TC 9-62
Figure 3-14. Reverse-biased PN Junction
3-29. As Figure 3-14 shows, the insulation gap formed by reverse biasing the varactor is
comparable to the layer of dielectric material between the plates of a common capacitor.
The formula (shown below) used to calculate capacitance could also be applied to both the
varactor and the capacitor. In this case, the size of the insulation gap of the varactor, or
depletion region, is substituted for the distance between the plates of the capacitor. By
varying the reverse-bias voltage applied to the varactor, the width of the "gap" may be
varied. An increase in reverse bias increases the width of the gap (d) that reduces the
capacitance (C) of the PN junction. Therefore, the capacitance of the varactor is inversely
proportional to the applied reverse bias.
AK
C=
d
Where:
A = plate area
K = a constant value
d = distance between plates
3-30. The ratio of varactor capacitance to reverse-bias voltage change may be as high as
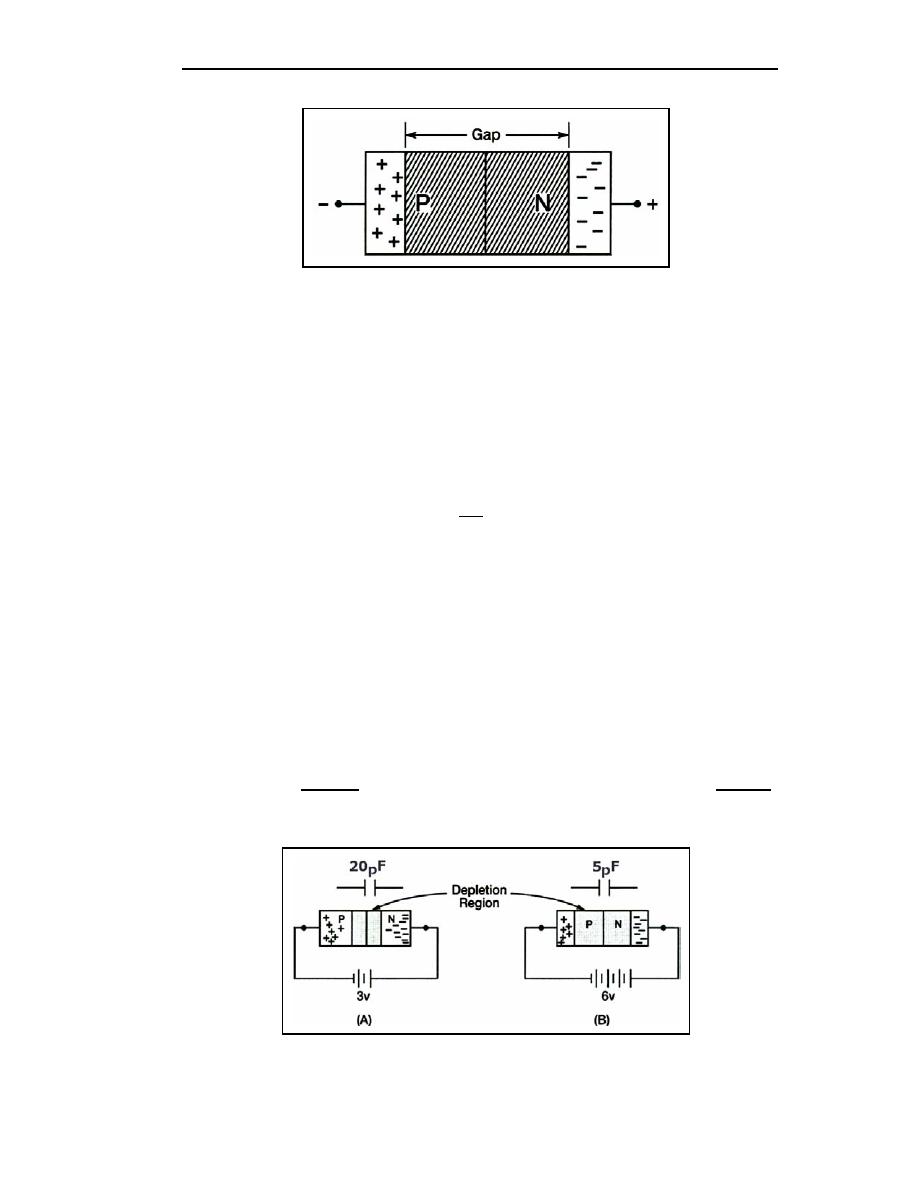
10 to 1. Figure 3-15 shows one example of the voltage-to-capacitance ratio. View (A)
shows that a reverse bias of 3 volts produces a capacitance of 20 picofarads in the varactor.
If the reverse bias is increased to 6 volts, as shown in view (B), the depletion region widens
and capacitance drops to 5 picofarads. Each 1-volt increase in bias voltage causes a 5
picofarad decrease in the capacitance of the varactor. The ratio of change is therefore 5 to
1. Of course any decrease in applied bias voltage would cause a proportionate increase in
capacitance, as the depletion region narrows. Notice that the value of the capacitance is
small in the picofarad range.
Figure 3-15. Varactor Capacitance Versus Bias Voltage
3-10
TC 9-62
23 June 2005



 Previous Page
Previous Page
