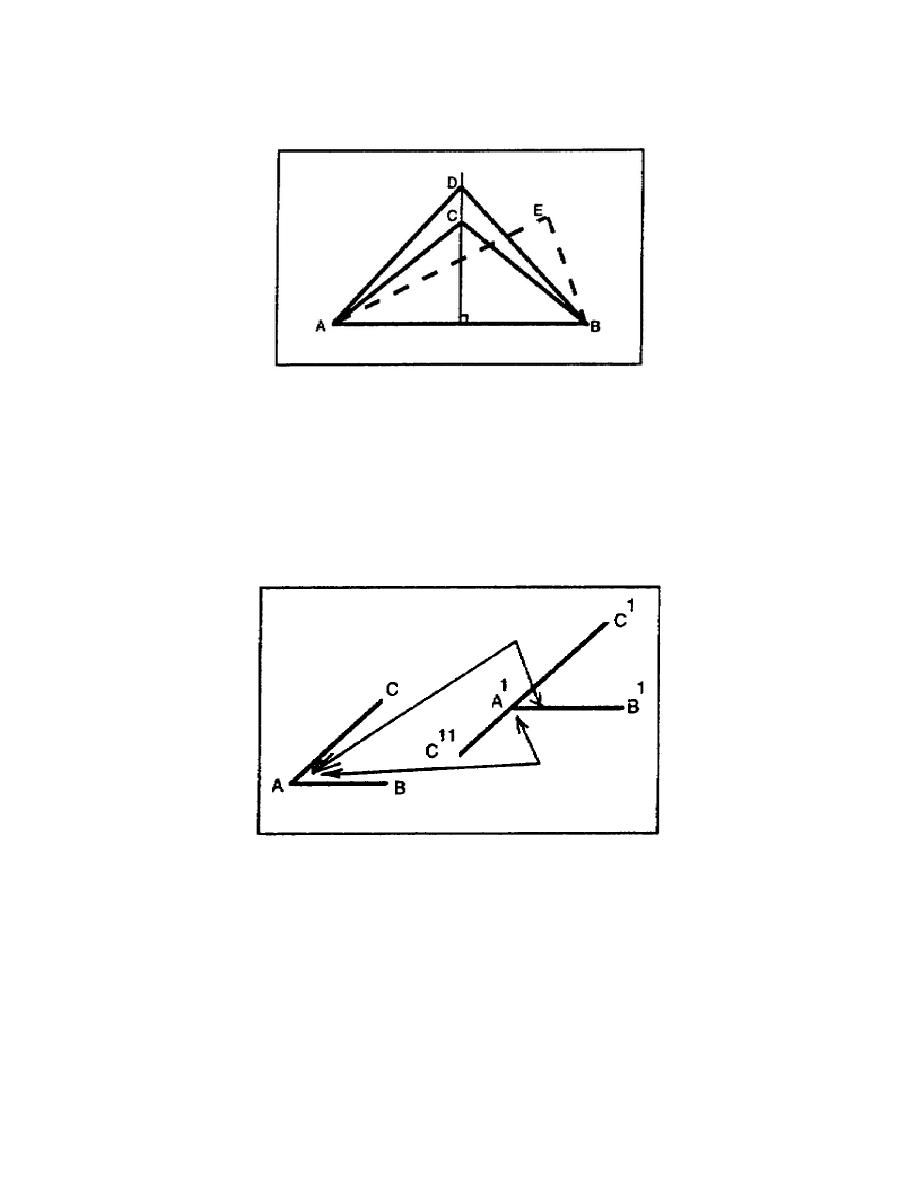
extremities of the line segment are unequal. Figure 3-15 shows that line AC is equal to BC and line AD
is equal to BD, but line AE is not equal to BE.
Figure 3-15. Points equidistant from line segment extremities
3-10. Theorems for Angles. The following theorems show the relationship of two angles whose
respective sides are either parallel or perpendicular to each other.
a. Theorem 1. If two angles have their sides respectively parallel, the angles are either equal or
supplementary, as shown in Figure 3-16. Line C1C11 is parallel with AC, and line A1B1 is parallel with
AB. Angle B1A1C1 is equal to BAC, and angle B1A1C11 is the supplement of B1A1C1; therefore, angle
B1A1C11 is also the supplement of BAC.
Figure 3-16. Parallel sides
b. Theorem 2. If two angles have their sides respectively perpendicular, the angles are either
equal or supplementary, as shown in Figure 3-17. Line C1C11 is perpendicular to AC, and line A1B1 is
perpendicular to AB. Angle B1A1C1 is equal to BAC, and angle B1A1C11 is the supplement of B1A1C1;
therefore, angle B1A1C11 is also the supplement of BAC.
EN0591
3-10



 Previous Page
Previous Page
