Figure 3-12. Parallel lines cut by a perpendicular line
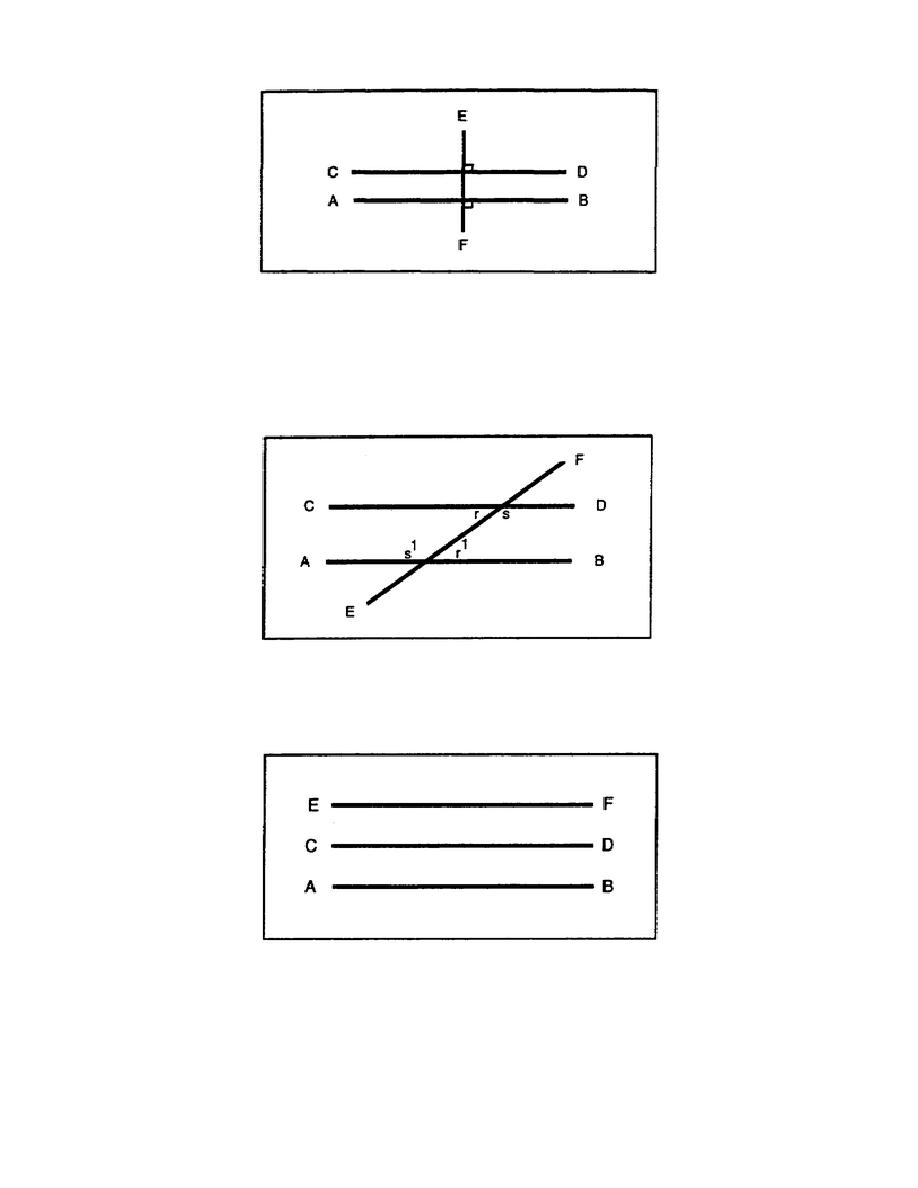
c. Theorem 3. If two parallel lines are cut by a transversal, the alternate interior angles are
equal. Therefore, when two lines are cut by a transversal and one pair of alternate interior angles are
equal, the two lines are parallel. In Figure 3-13, lines AB and CD are parallel and line EF is the
transversal. Interior angles r and r1 are equal, and interior angles s and s1 are equal.
Figure 3-13. Parallel lines cut by a transversal
d. Theorem 4. Straight lines that are parallel to the same line are parallel to each other. In
Figure 3-14, if line CD is parallel to AB and line EF is parallel to AB, then line CD is parallel to EF.
Figure 3-14. Parallel lines
e. Theorem 5. Any point on a perpendicular bisector of a line segment is equidistant from the
extremities of the line segment. The distances from any point not on the perpendicular bisector to the
3-9
EN0591



 Previous Page
Previous Page
