(3) The third angles of two triangles are equal if the two angles of one triangle are equal to
the two angles of the other triangle.
(4) The right triangles are equal if the side and the acute angle of one triangle are equal to the
corresponding side and the acute angle of the other triangle.
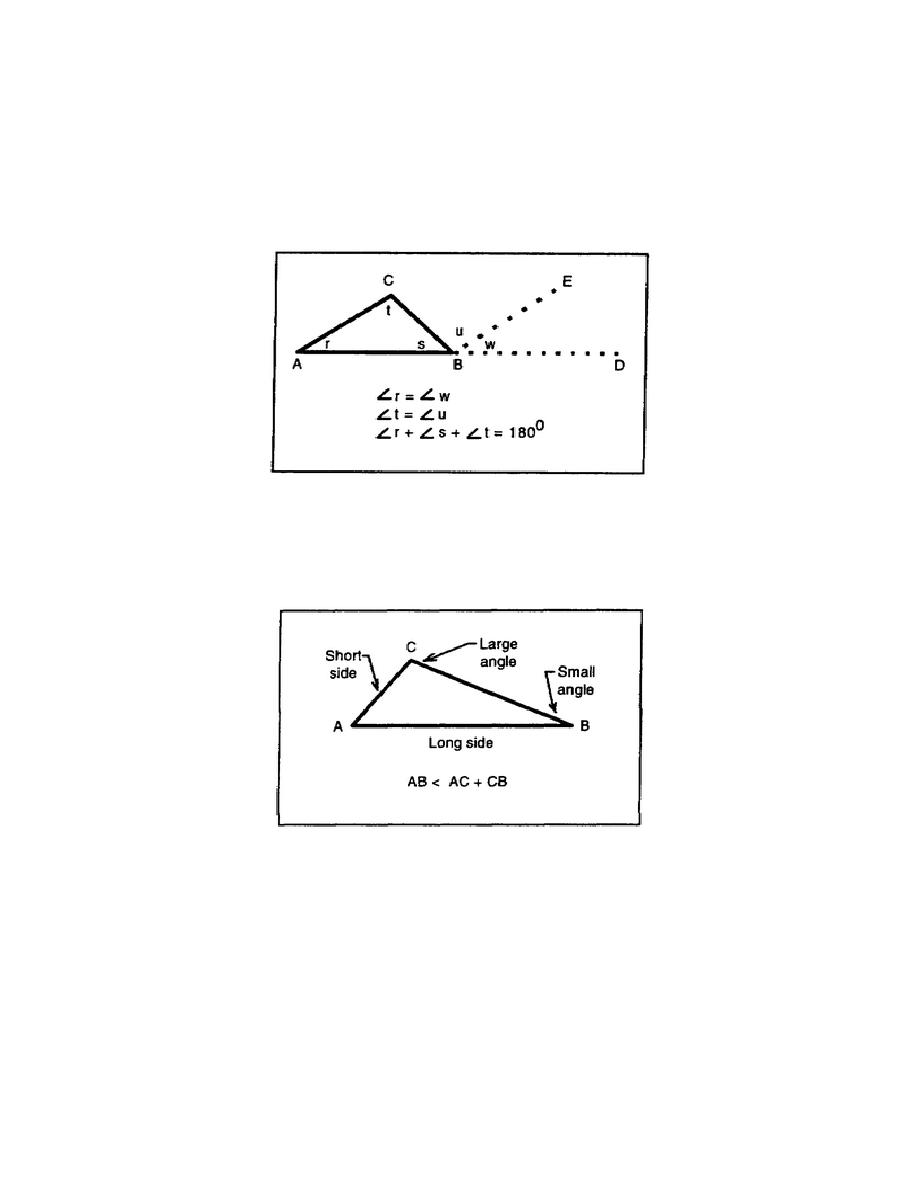
(5) Any exterior angle of a triangle is equal to the sum of the two opposite interior angles.
Figure 3-19. Sum of angles equal 180
b. Theorem 2. Any side of a triangle is less than the sum of the other sides. This theorem can
be proved by using the postulate in paragraph 3-6a. As shown in Figure 3-20, side AB is a straight line
and the other two sides, AC and CB, form a bent line between points A and B.
Figure 3-20. Relative sizes of angles and sides
c. Theorem 3. If two sides of a triangle are equal, the angles opposite these sides are equal, as
shown in Figure 3-21. Conversely, if two angles of a triangle are equal, the sides opposite these angles
are equal. The following corollaries can be derived from this theorem:
EN0591
3-12



 Previous Page
Previous Page
