Figure 3-17. Perpendicular sides
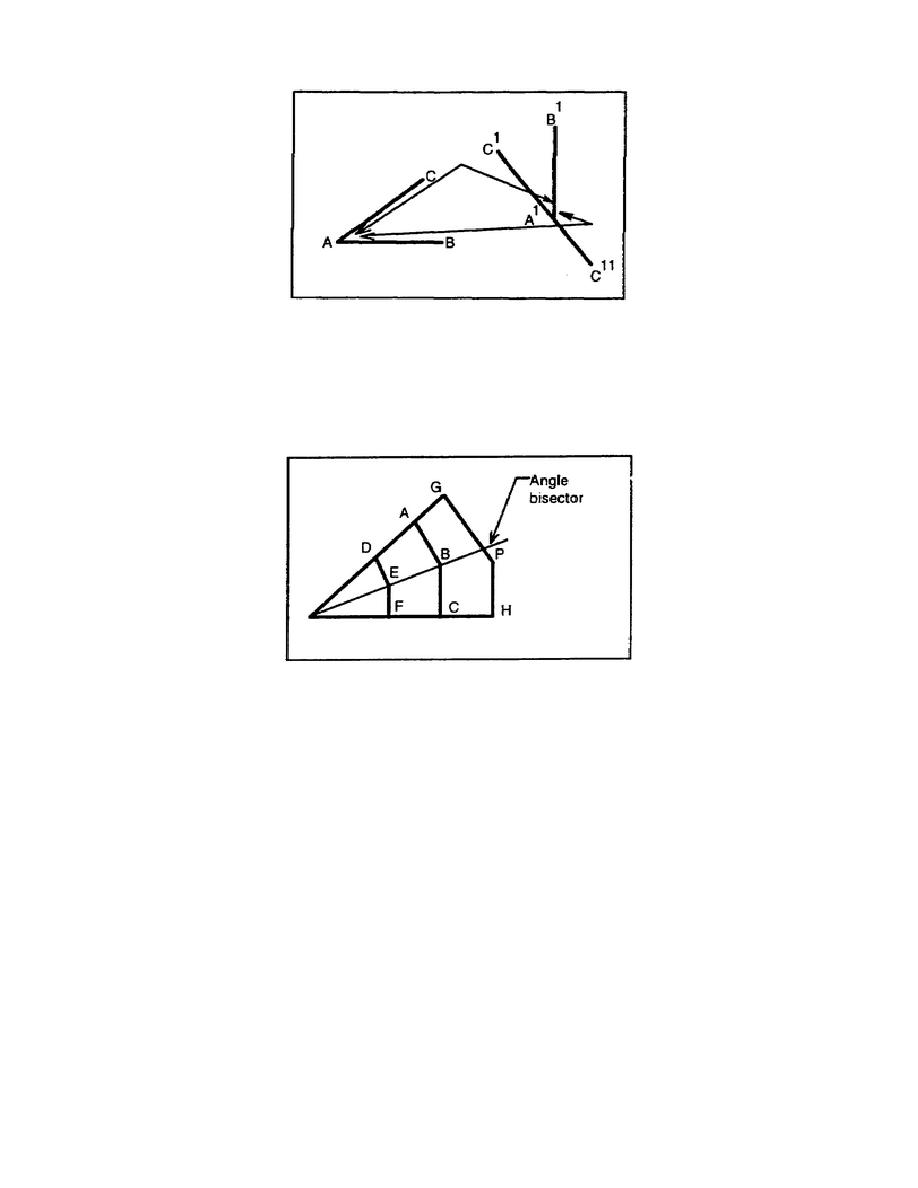
c. Theorem 3. Every point on an angle bisector is equidistant from the sides of the angle. The
distances from a point not on the angle bisector to the sides of the angle are unequal. Figure 3-18 shows
that line AB is equal to BC and line DE is equal to EF, but line GP is not equal to PH. A corollary for
this theorem is that all points within an angle that are equidistant from its sides lie in the angle bisector.
Figure 3-18. Points equidistant from the sides of an angle
3-11. Theorems for Triangles. The following theorems are for the basic relationships of the angles
and sides of a triangle.
a. Theorem 1. The sum of the angles of a triangle is equal to two right angles. This theorem
can be proved by using the illustration shown in Figure 3-19, page 3-12. Line AB is extended to D, and
line BE is parallel to AC. Angle r is equal to w, and angle t is equal to u. Since angle s plus angle u plus
angle w equals 180€, angle r plus angle t plus angle s also equals 180€ or two right angles. The
following corollaries can be developed from this theorem:
(1) The sum of the two acute angles of a right triangle is equal to a right angle.
(2) A triangle cannot have more than one right angle or more than one obtuse angle.
3-11
EN0591




 Previous Page
Previous Page
