TC 9-62
Where:
R represents the resistance of the charge or discharge path.
C represents the capacitance of the capacitor.
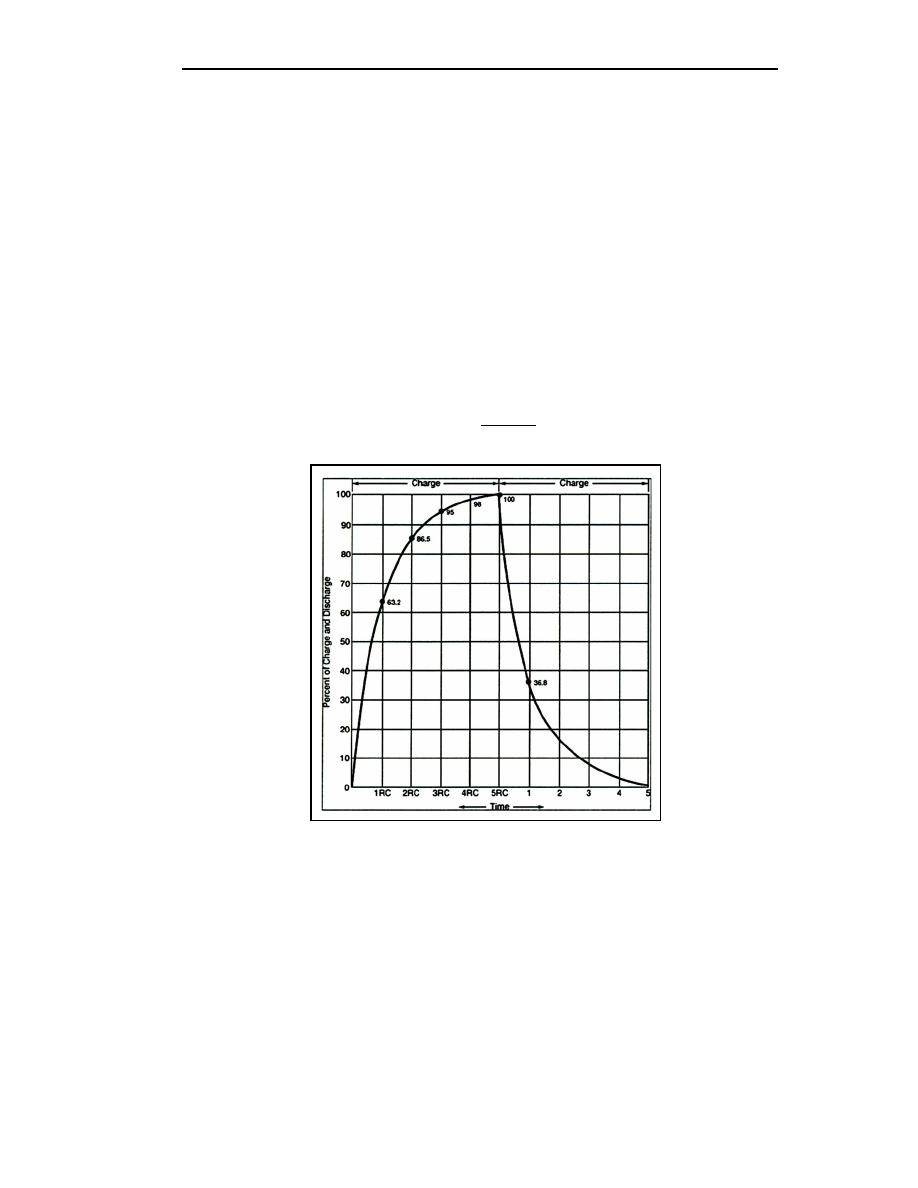
A capacitor is considered fully charged after five RC time constants (see Figure 4-11). You
can see that a steady DC output voltage is obtained when the capacitor charges rapidly and
discharges as slowly as possible.
4-33. In filter circuits the capacitor is the common element to both the charge and the
discharge paths. Therefore, to obtain the longest possible discharge time, you want the
capacitor to be as large as possible. Another way to look at it is that the capacitor acts as a
short circuit around the load (as far as the AC component is concerned) and since the larger
following formula).
1
XC =
2πfC
Figure 4-11. RC Time Constant
4-34. Let us look at inductors and their application in filter circuits. Remember, AN
INDUCTOR OPPOSES ANY CHANGE IN CURRENT. A change in current through an
inductor produces a changing electromagnetic field. The changing field, in turn, cuts the
windings of the wire in the inductor and thereby produces a counterelectromotive force. It
is the cemf that opposes the change in circuit current. Opposition to a change in current at a
inductor is determined by the applied frequency and the inductance of the inductor (see the
following formula).
XL = 2 π f C
4-12
TC 9-62
23 June 2005



 Previous Page
Previous Page
