TC 9-62
Where:
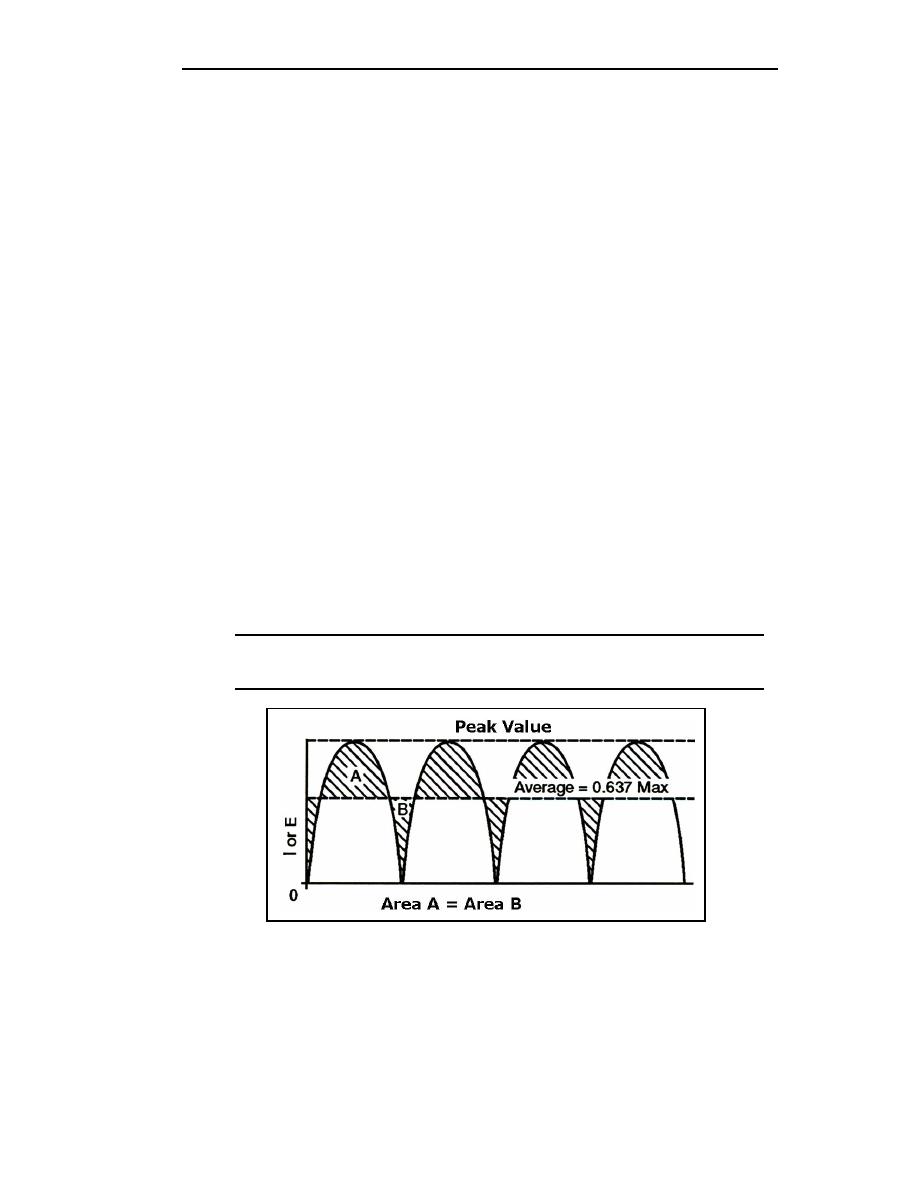
Emax = the peak value of the load voltage pulse.
Eavg = 0.637 x Emax (the average load voltage).
Imax = the peak value of the load current pulse.
Iavg = 0.637 x Imax (the average load current).
supply a full-wave rectifier is 300 volts. Find the average load voltage (ignore the drop
across the diode).
Solution: Since the total secondary voltage (ES) is 300 volts, each diode is supplied
one-half of this value, or 150 volts. Since the secondary voltage is an RMS value, the
formula for the peak load voltage is as follows:
Emax = 1.414 x Es
Emax = 1.414 x 150
Emax = 212 volts
The average load voltage is computed as follows:
Eavg = 0.637 x Emax
Eavg = 0.637 x 212
Eavg = 135 volts
NOTE: If you have problems with this equation, review the portion of
TC 9-60 that pertains to this subject.
Figure 4-7. Peak and Average Values for a Full-wave Rectifier
4-22. Remember, every circuit has advantages and disadvantages. The full-wave rectifier
is no exception. In studying about the full-wave rectifier, you may have found that by
doubling the output frequency, the average voltage has doubled, and the resulting signal is
much easier to filter because of the high ripple frequency. The only disadvantage is that the
peak voltage in the full-wave rectifier is only half the peak voltage in the half-wave
4-8
TC 9-62
23 June 2005



 Previous Page
Previous Page
