______________________________________________________________ Solid State Power Supplies
alternating components of the signal around the load (to ground). Resistors are used in
place of inductors in low current applications.
4-29. Reviewing the properties of a capacitor we will see that a capacitor opposes any
change in voltage. The opposition to a change in voltage is called capacitive reactance (XC)
and is measured in ohms. The capacitive reactance is determined by the frequency (f) of
the applied voltage and the capacitance (C) of the capacitor. Use the following formula to
make this determination:
1
.159
XC =
or
2 π fC
fC
4-30. You can see from the formula that if frequency or capacitance is increased, the XC
decreases. Since filter capacitors are placed in parallel with the load, a low XC will provide
better filtering than a high XC. To do this, a better shunting effect of the AC around the
load is provided (see Figure 4-10).
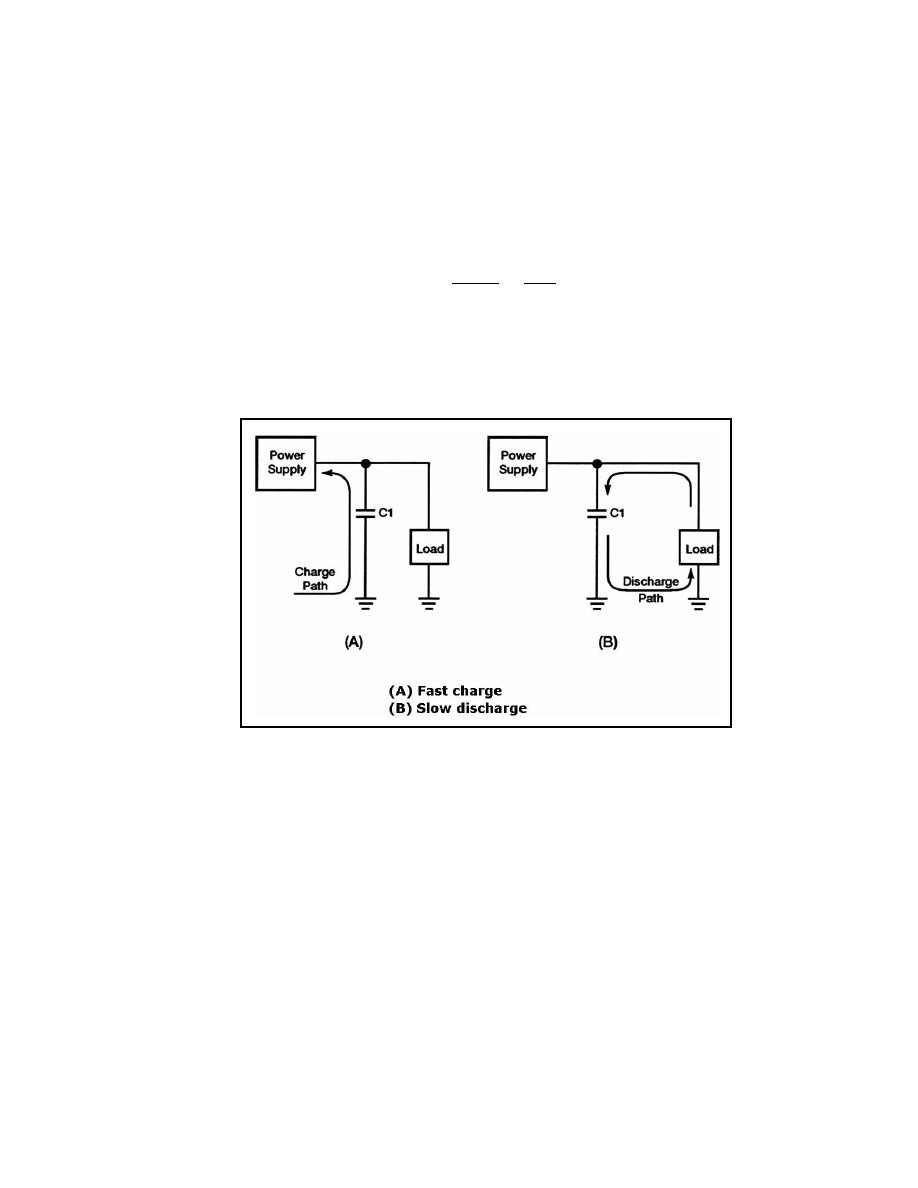
Figure 4-10. Capacitor Filter
4-31. To obtain a steady DC output, the capacitor must charge almost instantaneously to
the value of applied voltage. Once charged, the capacitor must retain the charge as long as
possible. The capacitor must have a short charge time constant. You can do this by keeping
the internal resistance of the power supply as small as possible (fast charge time) and the
resistance of the load as large as possible (slow discharge time). Figure 4-10, view (A),
shows the fast charge time and view (B) shows the slow discharge time.
4-32. Remember learning from basic electricity that a one time constant is defined as the
time it takes a capacitor to charge to 63.2 percent of the applied voltage or to discharge to
36.8 percent of its total charge. This action can be expressed by the following equation:
t = RC
23 June 2005
TC 9-62
4-11




 Previous Page
Previous Page
