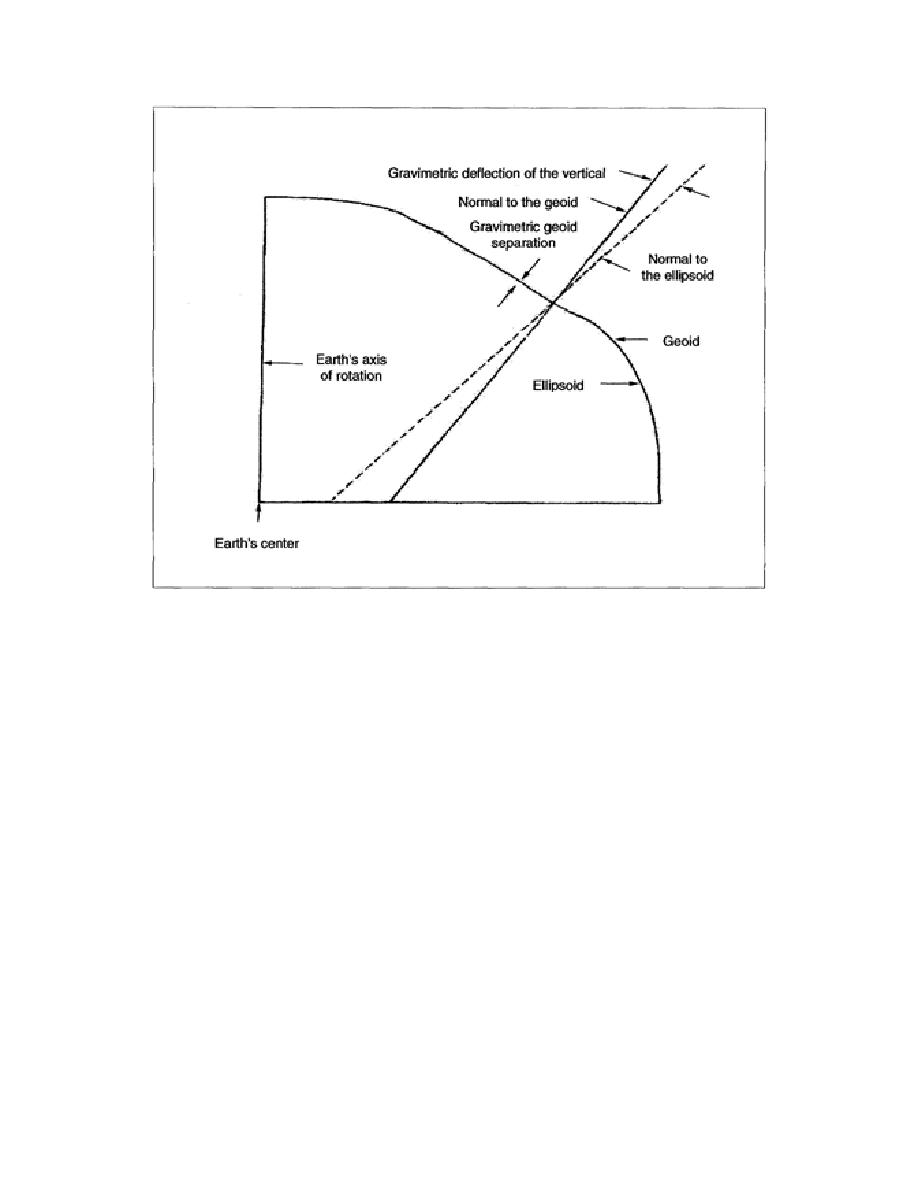
Figure 1-15. Products of the Gravimetric Method
(2) Computing the undulations of the geoid and deflections of the vertical requires extensive
gravity observations. The areas immediately surrounding the computing point require a dense coverage
of gravity observations. Detailed data must be obtained from distances out to 500 miles. A less dense
network is required for the rest of the earth. The deflections and undulations computed from
information obtained from these extensive observations are considered absolute values when referred to
an earth-centered, referenced ellipsoid. In other words, the axis of rotation for the ellipsoid coincides
with the rotation axis of the earth, and the geometrical center of the ellipsoid coincides with the earth's
center of gravity (Figure 1-15).
n. The collection of gravity observations requires measuring the gravity at or near the earth's
surface. The ultimate goal is to obtain a good distribution of gravity observations over the entire surface
of the earth. Since 70 percent of the earth's surface is water, this is not an easy task. Consequently,
geodesists are forced to use Stokes's theorem method to determine geoid separation in areas where
gravity observations have not been made.
o. The absolute acceleration of gravity is usually measured with a pendulum apparatus. The
swinging period of a pendulum is accurately timed, and from this time interval the value of gravity is
computed. Pendulum measurements require lengthy observations, and the average period of swing must
be determined from several
EN0593
1-22



 Previous Page
Previous Page
