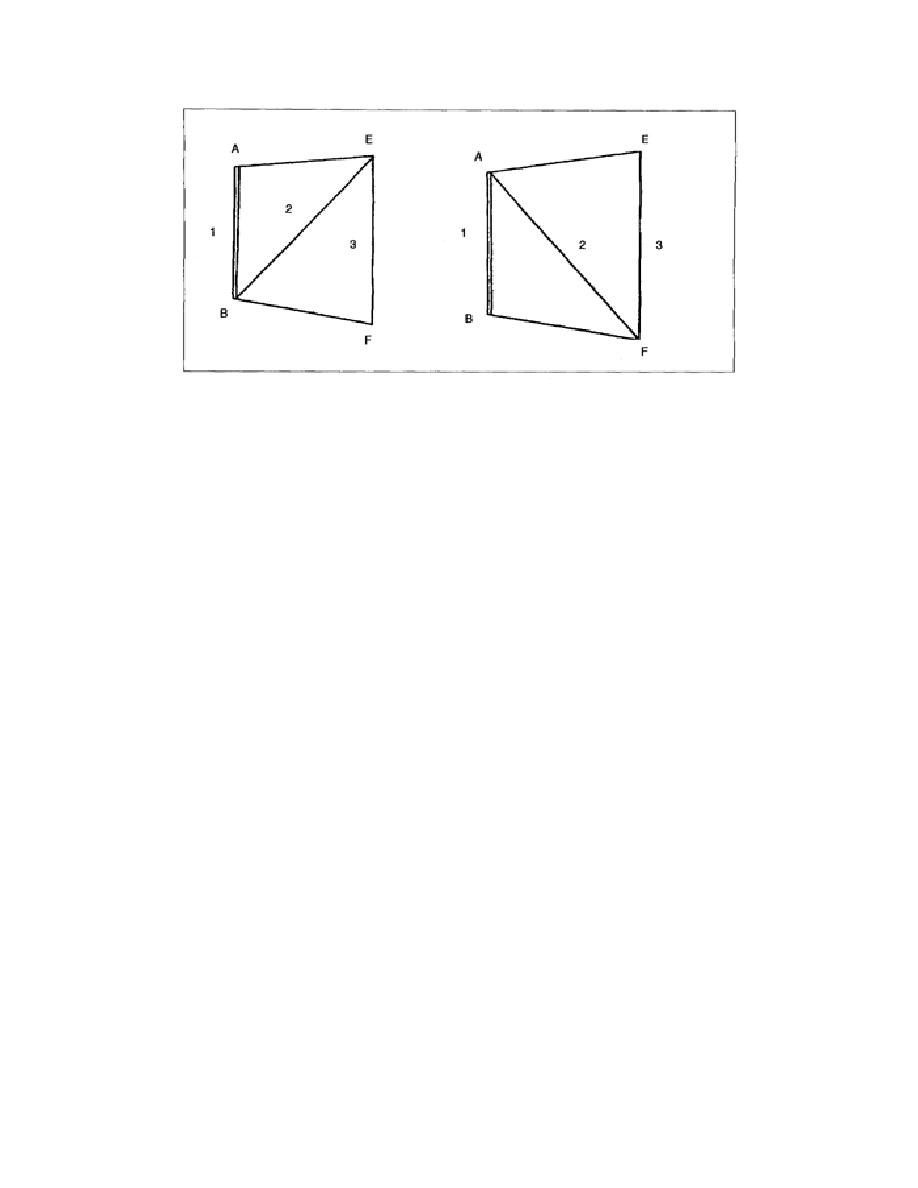
Figure 2-3. Methods Used to Compute Line EF
The illustrations in Figure 2-3 are quadrilaterals. This is the simplest and most economical figure used
to give a double determination or check on the length of the line, as computed through the quadrilateral.
This figure will be used as the go forward line or base for the succeeding figure. In first-order
triangulation, the figures must be such that they afford a double check and all stations are occupied.
Single triangles should not be used in first-order triangulation and only rarely in second-order
triangulation.
2-36. Acceptable Error of Angle Measurements. Together with the criterion of length agreement
between bases, and almost equal in importance, are the requirements limiting the acceptable error of
angle measurements. The limits imposed on angular errors serve to maintain a uniform accuracy along
the chain of triangles. The specifications for procuring the required accuracy make use of other criteria,
such as the number and strength of the geometrical figures between adjacent bases, the observation of
astronomical azimuths at specified intervals, and the accuracy of baseline measurements. All of these
requirements are subsidiary to the controlling tests of the agreement between the measured and the
computed length of a base and the limits specified for angle errors, and they are essential in securing
sustained accuracy and control.
2-37. Standards of Accuracy. In review, the following standards of accuracy are rigidly applied to
field observations in order to obtain consistent results in procuring the required precision. The
requirements will vary, depending on the classification of the triangulation, be it first order or second
order.
Baseline-measurement accuracy.
The strength of a single figure in a network.
The sum of the strengths of figures (R1) between baselines.
The maximum single-triangle closure.
The average triangle closure between bases.
2-21
EN0593



 Previous Page
Previous Page
