e. Theorem 5. In a right triangle, if a perpendicular line is drawn from the vertex of the right
angle to the hypotenuse, the perpendicular line is the mean proportion between the segments of the
hypotenuse. The following proportion can then be written for the right triangle shown in Figure 3-35:
AD : CD = CD : DB
Figure 3-35. Right angles
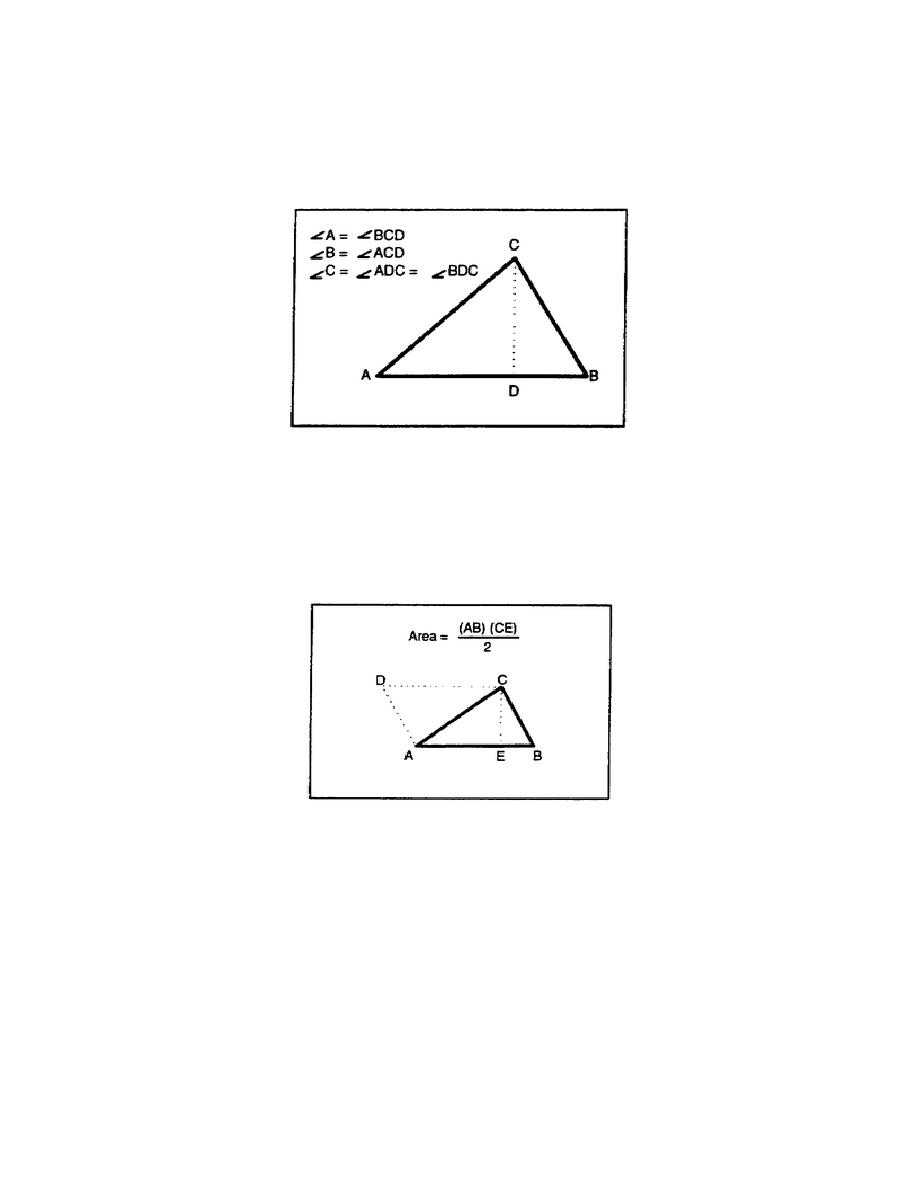
3-16. Theorem for the Area of a Triangle. The area of a triangle is equal to one-half the product of
its base and its altitude. This theorem can be proved with the aid of Figure 3-36, which shows a
parallelogram (ABCD) whose sides are parallel to two sides of triangle ABC. Triangles ABC and ACD
are equal; therefore, the area of triangle ABC is one-half the area of parallelogram ABCD. The area of
parallelogram ABCD is the product of triangle ABC's base and altitude.
Figure 3-36. Area of a triangle
3-17. Equating like quantities. By using the theorems for similar triangles, you can often determine
distances that cannot be readily measured directly. For example, the antenna reflector in Figure 3-37
casts a shadow on the ground that is 35 feet 9 inches from a point directly beneath the antenna pole. At
the same time, a yardstick in a vertical position casts a shadow that is 1 foot 2 inches in length. Since
light from the sun strikes both the antenna pole and the yardstick at the same angle, angles C and C1 are
equal, and triangles ABC and A1B1C1 are similar. Using the skills of equating like qualities that you
learned in Lesson 2 under Ratios and Proportions, set up the problem as follows:
EN0591
3-20



 Previous Page
Previous Page
