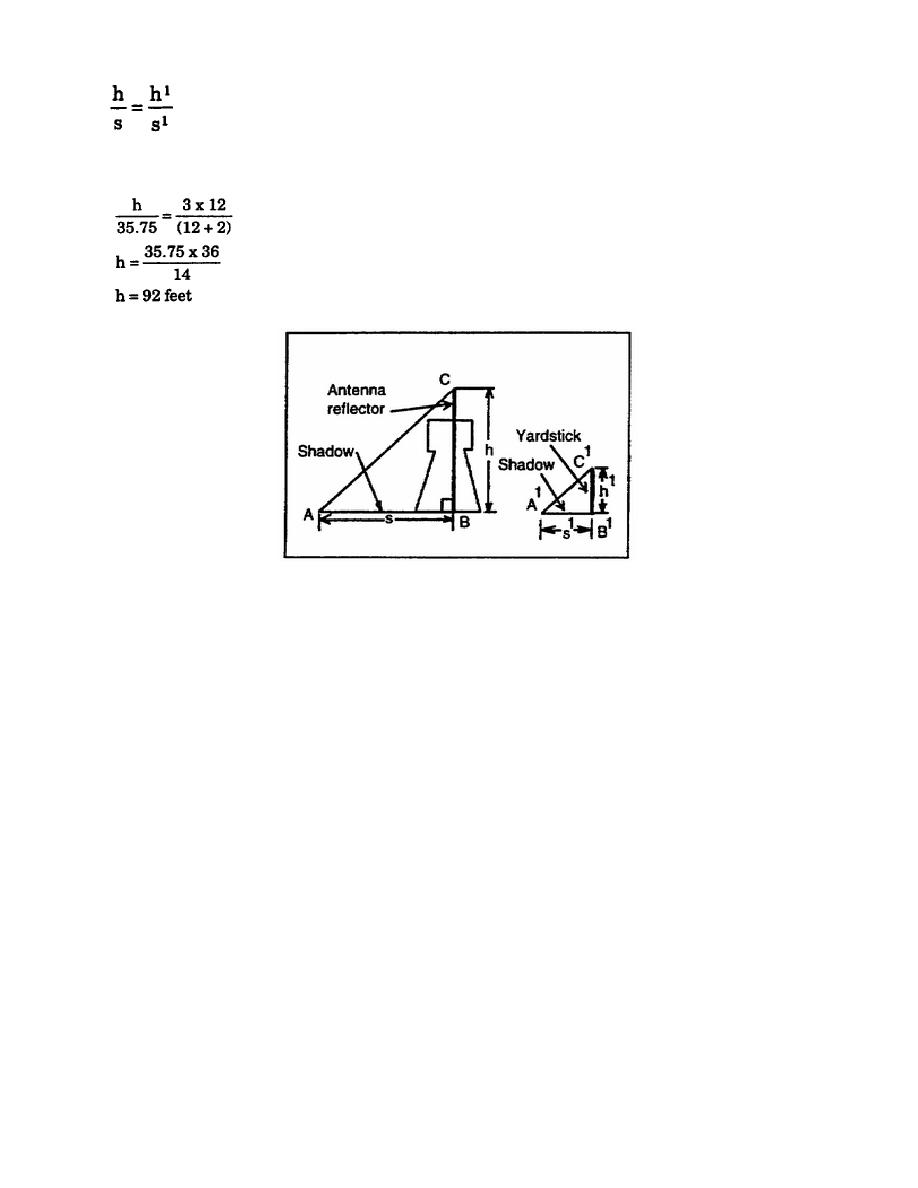
Then, substituting known values and solving for h:
Figure 3-37. Height of antenna reflector
PART F - REVIEW OF GEOMETRY
problems is somewhat limited, many of its terms, postulates, theorems, and corollaries have an
important bearing on trigonometric computation. The triangle, as you know, plays a very important part
in the profession of surveying. For that reason, the following paragraphs will reference you back to
pertinent portions of the text in this lesson.
a. In paragraph 3-1, various terms useful in solving geometric problems were defined. Among
these were a point, lines (both straight and curved), and flat surfaces. Careful analysis showed that both
lines and surfaces were actually generated by a point moving in a straight or a constantly changing
direction. In one sense, a line could be considered as the edge view of a flat surface; thus, a straight line
could very well be one edge of a flat plane while a curved line could represent one edge of a curved
surface.
In plane geometry, a flat plane can be developed by moving a straight line in a direction 90€ to its length
or by fixing one end of the straight line and swinging its free end a designated distance. By such
controlled movement, a segment of a circle that closely resembles a triangle or a complete circle (both of
which are flat planes) can be generated from a straight line. The distance that such a straight line is
allowed to swing in an arc is measured in special units which are known as degrees, minutes, or seconds.
Each of these measurement units is useful when measuring or determining the size of an angle.
3-21
EN0591



 Previous Page
Previous Page
