Two sides and the included angle.
Three sides.
a. Any triangle can be solved by dividing the triangle into two right triangles and applying the
formulas for solving right triangles. To eliminate much of the work involved in solving two right
triangles, formulas or laws have been derived that enable you to solve oblique triangles directly.
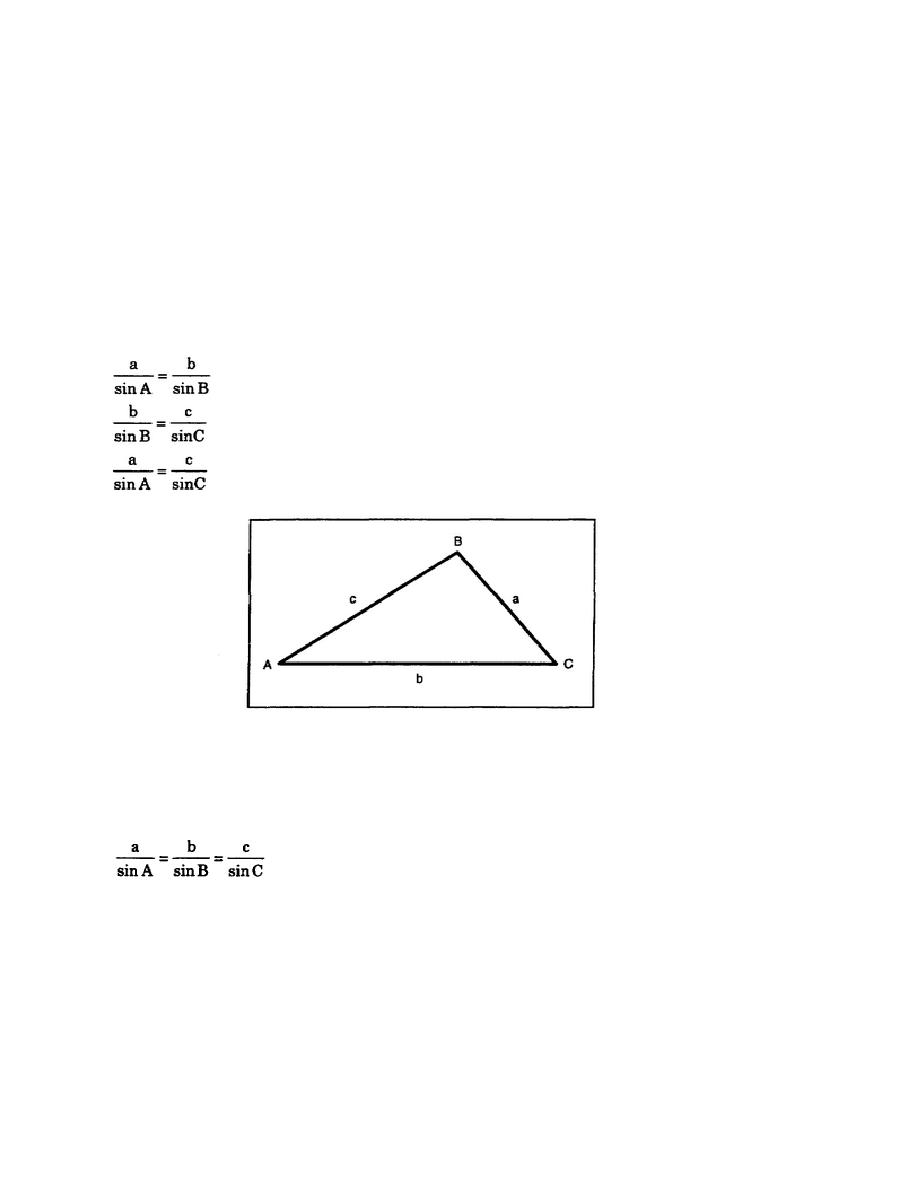
b. The sine law states that in any triangle, the sides are proportional to the sines of their
opposite angles. This law also applies in solving triangles where the given information includes one
side and two angles or two sides and an opposite angle. When applying the sine law to Figure 4-17, you
get various relationships and equations. For example:
Figure 4-17. The oblique triangle
c. Since you can solve any triangle in which three parts are known, including a side, it is
necessary to set up a relationship between any two sides and their opposite angles. These relationships
are as follows:
d. The cosine law states that in any triangle, the square of any side is equal to the sum of the
squares of the other sides minus twice the product of those two sides time the cosine of the angle
included between them. This law is adaptable to solving triangles where two sides and the included
angle are given and it is desired to find the length of the third side. Three situations exist where the
cosine law can be applied. They are as follows:
EN0591
4-24



 Previous Page
Previous Page
