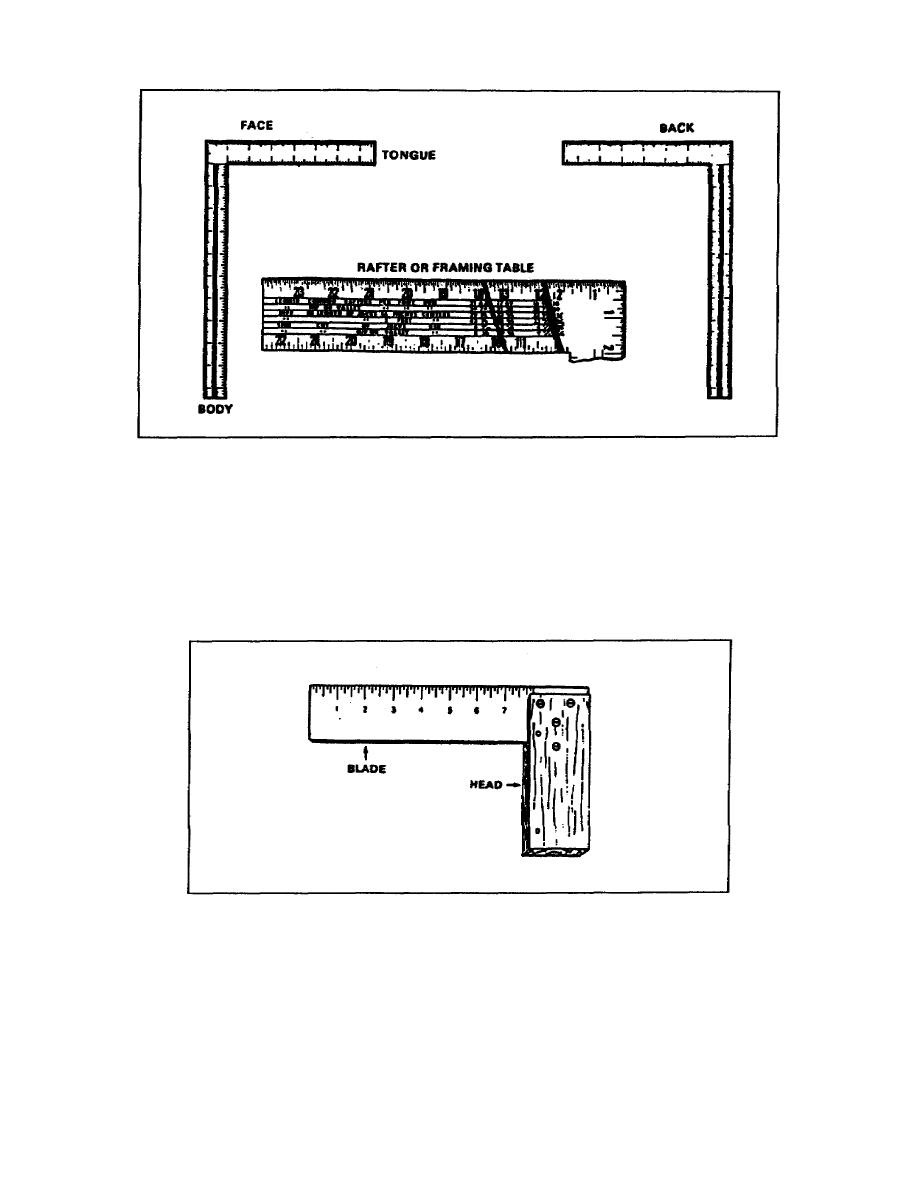
Figure 2-45.
Framing square
a. Try Square. The try square (Figure 246) is so called because
of frequent use as a testing tool when squaring up wood stock. It
consists of a steel blade 8 inches long at right angle to the stock,
which is usually made of hardwood and faced with brass to preserve
the wood from damage. The blade usually has a scale divided into
eighths of an inch.
Figure 2-46.
Try square
b. Miter Square. The term miter means any angle except a right
angle, but as applied to squares mean an angle of 45 degrees
(Figure 247). It is similar to a try square, but the stock
of a miter square has an angle or 45 degree set in the
EN5155
2-24
Previous Page
