station is (K/2)2 x 0.0676, or one-fourth at one end only. In the field, the method generally amounts to a
determination of an equal signal height for both stations so that the sight line clears the obstruction.
Signal heights are nearly always computed in this way. Sometimes a higher signal is specified at one
station for some other line than the one under consideration. This permits a lower signal at the opposite
end of the line. The amount one signal may be reduced in height for a certain increase of the other is
proportional to the distance of the two stations from the obstruction. The station nearest to the
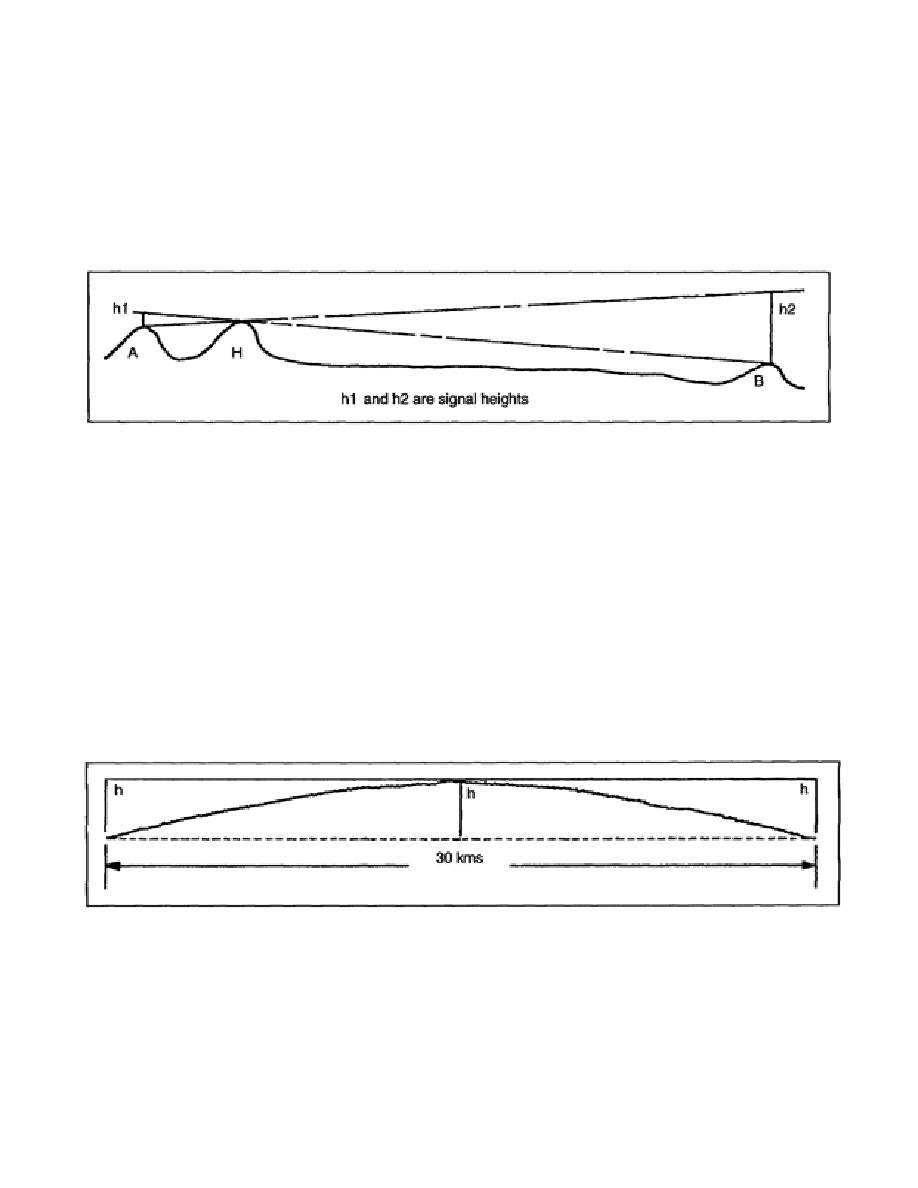
obstruction requires the least signal height to provide a clear line of sight. Figure 2-5 illustrates where
h1 and h2 are signal heights required at stations A and B respectively, to clear obstruction H.
Figure 2-5. Clearance of Obstruction
e. Occasionally, a series of obstructions may occur along a line of sight that may not be detectable
through inspection. A lower obstruction near the middle of the line may require higher signals to clear
than a higher obstruction near the end. The simplest way to determine a critical obstruction is to
compute the signal heights for each one in turn. The following examples illustrate typical problems:
Example 1. Two stations are at water level on opposite shores of a 30-kilometer-wide bay. What is
the height (h) of equal signals required to make the line of sight graze the surface of the water?
According to the formula, h = (K/2) 2 x 0.0676 = (30/2) 2x 0.0676 = 15.2 meters. Figure 2-6 shows h as
the distance of a line joining the stations (passing below the earth's surface). Because the obstruction is
equidistant from the two stations, h will also be the required height of equal signals at the two ends
needed to clear the line of sight. In actual practice, it is generally necessary to provide a certain amount
of clearance over obstructions in order to reduce horizontal refraction.
Figure 2-6. Signal Heights for a Line Over Water
Example 2. Figure 2-7 shows an example of two end stations not at the same elevation, with the
obstruction not centered at a point midway between them. When applying the formula, first determine
the amount of curvature at the obstruction at
EN0593
2-32


 Previous Page
Previous Page
