(13) BK is the altitude and BD is the base of both rectangle BDJK and triangle CBD.
(14) The area of triangle CBD is one-half the area of rectangle BDJK. Therefore, the areas of
rectangle BDJK and square FBCG are equal.
(15) The area of square ABDE is equal to the sum of the areas of the two rectangles (AKJE
and BDJK). Therefore, the area of square ABDE is also equal to the sum of the two squares (AIHC and
FBCG).
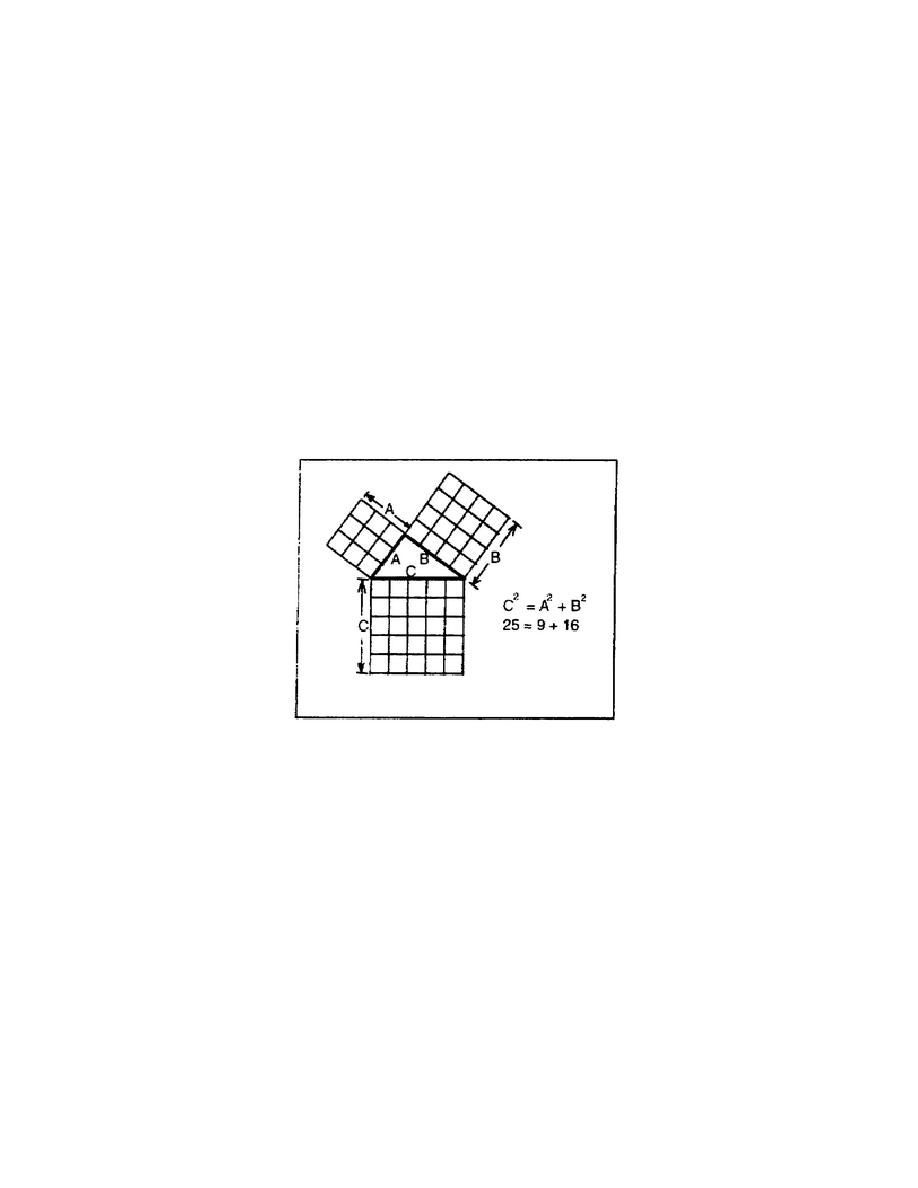
b. A special case of the right triangle, where each side can be divided into an integral number of
basic units, is shown in Figure 3-32. The length of side A is three units, the length of side B is four
units, and the length of the hypotenuse (side C) is five units. This triangle, called a 3-4-5 right triangle,
is often used to mark out long sides with an included right angle. Triangles with sides that are multiples
of 3, 4, and 5 (such as 15, 20, and 25) are also considered to be 3-4-5 right triangles. There are other
right triangles whose sides can be divided into an integral number of basic units, one of which has sides
that are 5, 12, and 13 units long. However, the 3-4-5 triangle is the easiest to remember and the most
commonly used.
Figure 3-32. Right triangle
3-15. Theorems for Similar Triangles. The corresponding angles of similar triangles are equal.
Equal triangles are similar, but similar triangles are not necessarily equal. The important relationship of
similar triangles is that a direct proportionality exists between corresponding sides. The following
theorems can be used to determine whether triangles are similar.
a. Theorem 1. A line parallel to one side of a triangle and intersecting the other two sides
divides these two sides proportionally. This condition is shown in Figure 3-33, in which the following
proportion exists:
AD : DC = BE : EC
EN0591
3-18


 Previous Page
Previous Page
