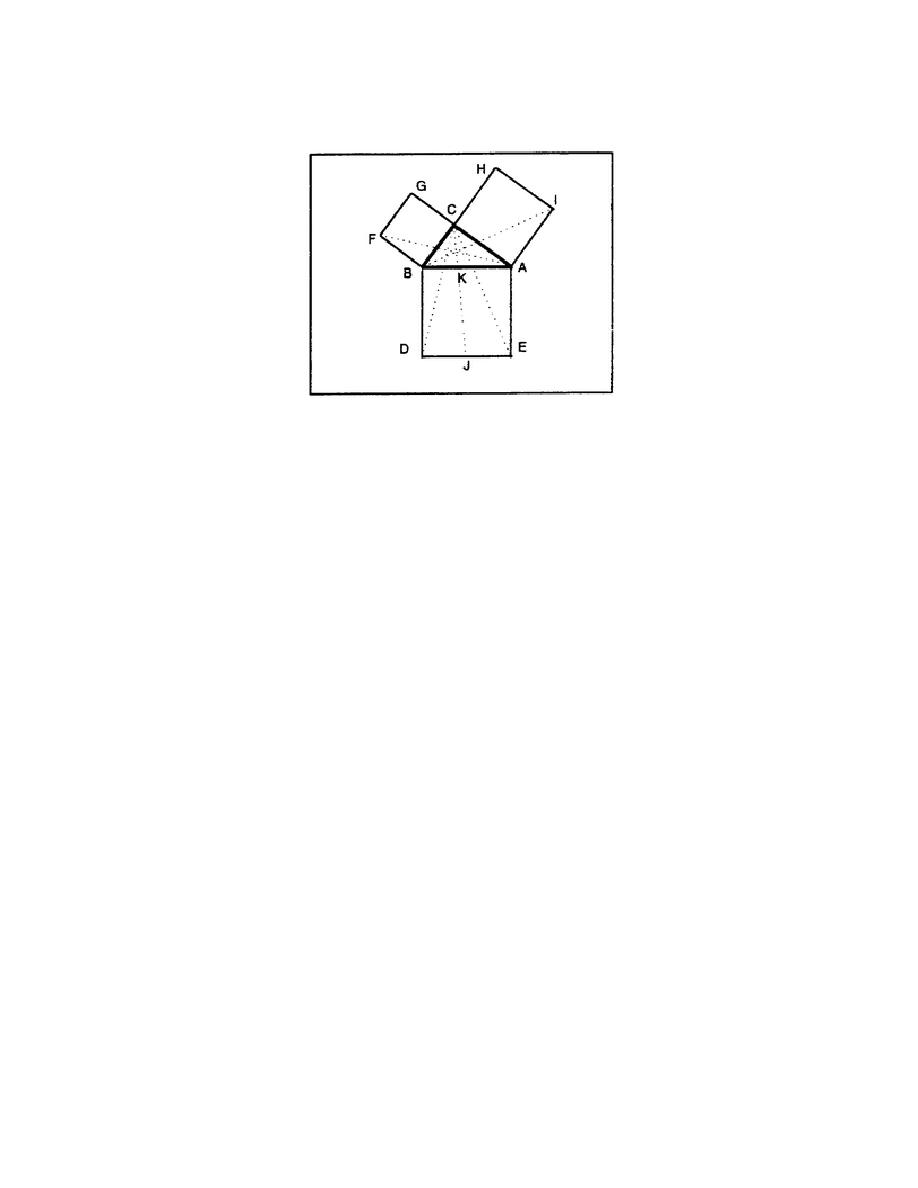
a. The Pythagorean theorem can be proved by using the illustration shown in Figure 3-31.
Examples are as follows:
Figure 3-31. Any right triangle
(1) Line AE is equal to AB and line Al is equal to AC of triangles CAE and IAB because
these lines are the sides of the squares.
(2) Angles EAC and BAI are equal.
(3) Triangles EAC and BAI are equal.
(4) AC is the altitude and AI is the base of both square AIHC and triangle AIB.
(5) The area of triangle AIB is one-half the area of square AIHC.
(6) AD is the altitude and AE is the base of both rectangle AKJE and triangle ACE.
(7) The area of triangle ACE is one-half the area of rectangle AKJE. Therefore, the areas of
rectangle AKJE and square AIHC are equal.
(8) Line BD is equal to AB and line BC is equal to BF of triangles CBD and FBA because
these lines are the sides of the squares.
(9) Angles CBD and FBA are equal.
(10) Triangles CBD and FBA are equal.
(11) BC is the altitude and FB is the base of both square FBCG and triangle FBA.
(12) The area of triangle FBA is one-half the area of square FBCG.
3-17
EN0591



 Previous Page
Previous Page
