b. Since there are 60" in 1 minute, this same process must be repeated for any remaining
minutes after the second division. Therefore, change the 2' remainder to 120" and add it to 14" (the
seconds shown in the original problem), which results in a sum of 134". Divide 134" by 3, which will
go 44 times with a remainder of 2". By converting this remainder to a decimal fraction (2/3 of a minute
equals 0.67 or rounding off to 0.7), you arrive at the answer desired. If there are no degrees or minutes
to be carried over, straight division is performed.
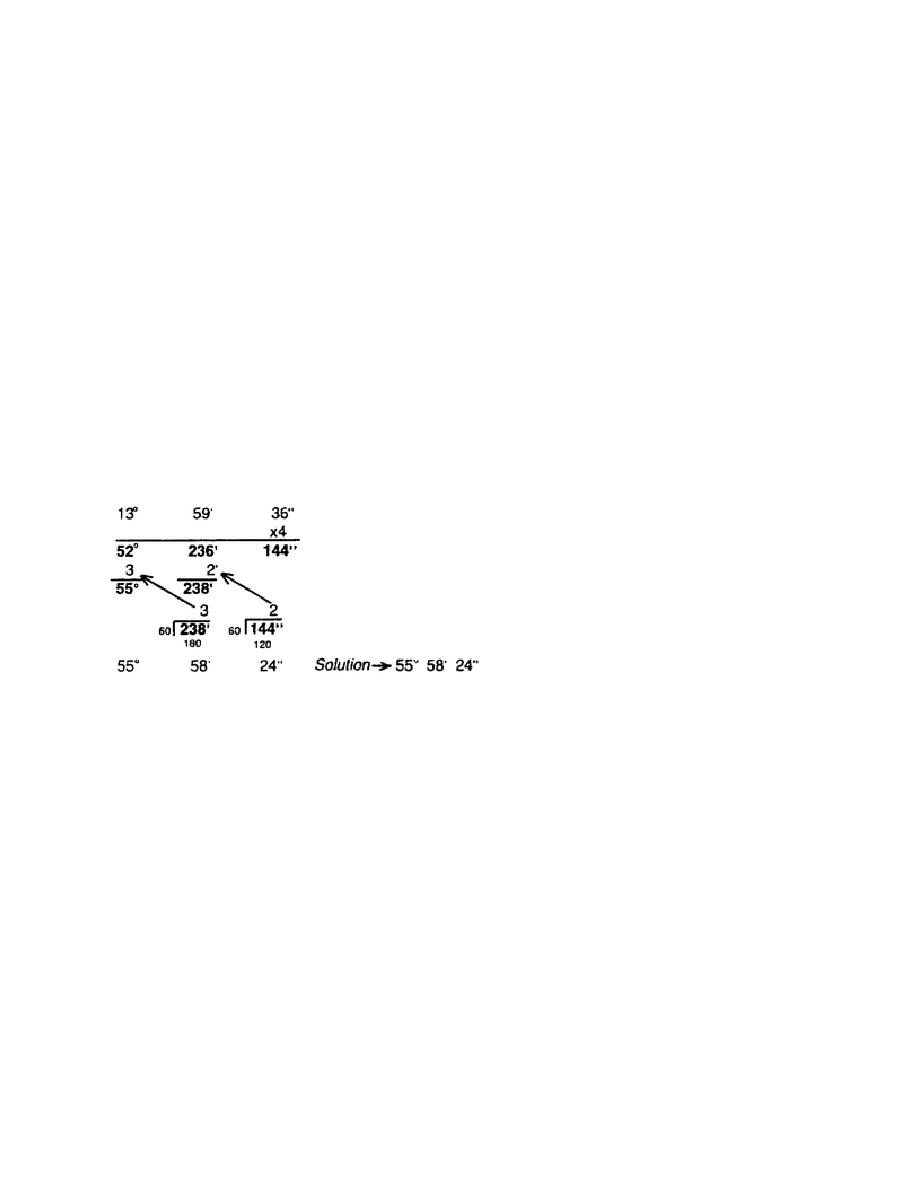
c. There will be times when the same angle must be used in field computations a number of
times. The simplest way to multiply an angle by a number is to perform each of the following steps:
Multiply the seconds by the number to determine the total number of seconds.
Multiply the minutes by the number to determine the total number of minutes.
Multiply the degrees by the number to determine the total number of degrees.
Example: Multiply 13 59' 36" by 4.
Solution:
d. If there are more than 59 seconds in the total seconds, the minutes must be extracted from the
seconds. This is done by dividing 60, the number of seconds in 1 minute, into the total number of
seconds. The quotient represents the number of minutes contained in the seconds, and the remainder
represents the odd number of seconds. This process is repeated to extract the degrees from the total
minutes if there are more than 59 after adding the minutes found in the seconds column. If there are any
degrees contained in the minutes after they have been extracted, they are added to the total amount of
degrees previously determined.
4-3. Converting Angles. Converting degrees, minutes, and seconds to degrees and decimal parts of a
degree is done in the following manner:
Divide the seconds by 60 to convert them to decimal parts of a minute.
4-3
EN0591



 Previous Page
Previous Page
