________________________________________________________________Wave Propagation
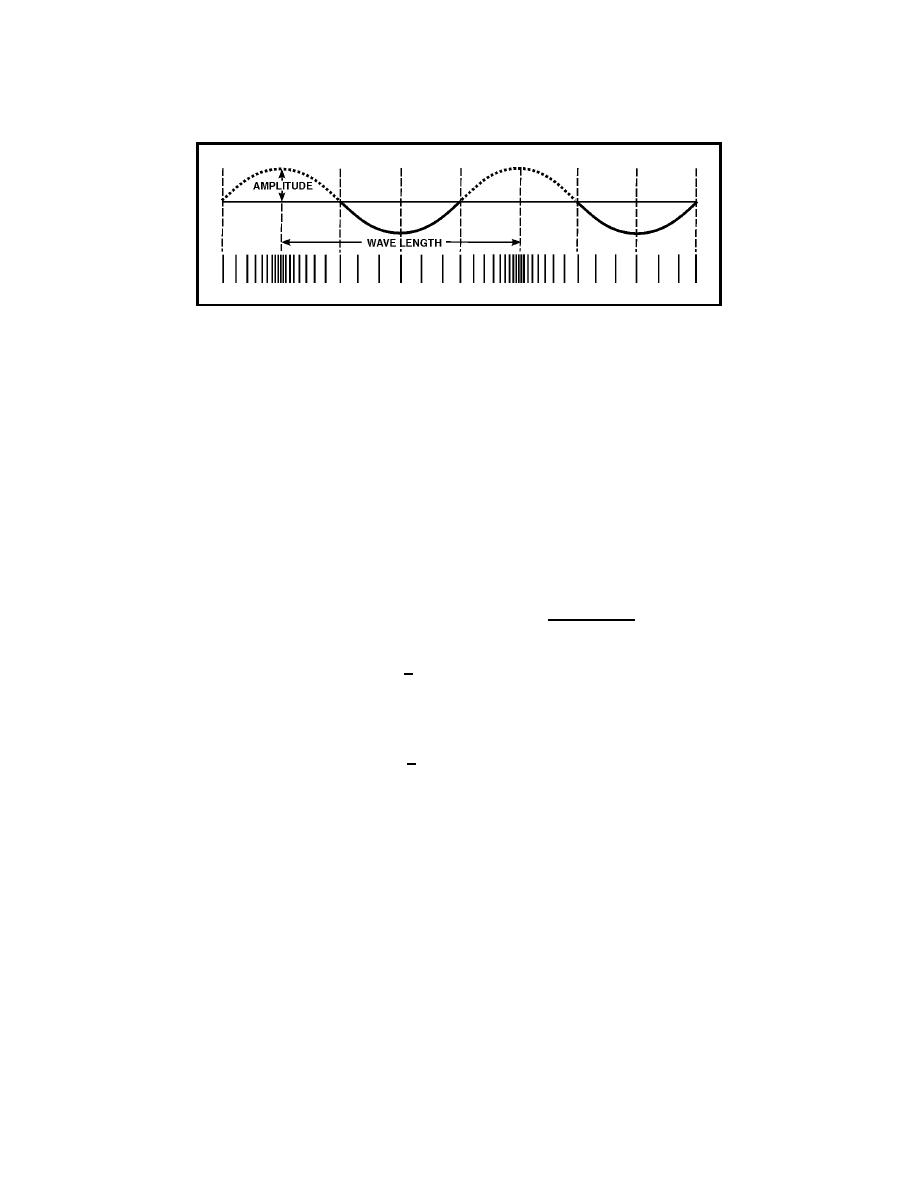
Figure 1-8. Longitudinal Wave Represented Graphically by a Transverse Wave
1-26. In the two types of wave motion described in the preceding discussion,
the following quantities are of interest:
The period, which is the time (T) in which one complete vibratory
cycle of events occurs.
The frequency of vibration (f), which is the number of cycles taking
place in one second.
The wavelength (λ), which is the distance the disturbance travels
during one period of vibration.
1-27. Now, consider the following concept. If a vibrating object makes a
certain number of vibrations per second, then 1 second divided by the number
of vibrations is equal to the period of time of 1 vibration. In other words, the
period, or time of 1 vibration is the reciprocal of the frequency. Thus--
1
Time (T) of one vibration =
frequency (f)
Or
1
T=
f
1-28. If you know the velocity of a wave, you can determine the wavelength
by dividing the velocity by the frequency. As an equation--
v
λ=
f
Where:
λ=
wavelength
v=
velocity of propagation
f=
frequency of vibration
1-29. When you use the above equation, be careful to express velocity and
wavelength in the proper units of length. For example, in the English system,
if the velocity (expressed in feet per second) is divided by the frequency
(expressed in cycles per second, or Hz), the wavelength is given in feet per
cycle. If the metric system is used and the velocity (expressed in meters per
second) is divided by the frequency (expressed in cycles per second), the
wavelength is given in meters per cycle. Be sure to express both the
wavelength and the frequency in the same units. (Feet per cycle and meters
per cycle are normally abbreviated as feet or meters because one wavelength
indicates one cycle.) Because this equation holds true for both transverse and
1-9


 Previous Page
Previous Page
