using both circles is 60' / 30 or 2 minutes. There are several ways to read the minute value using both
circles. These additional values are demonstrated and explained in the following examples:
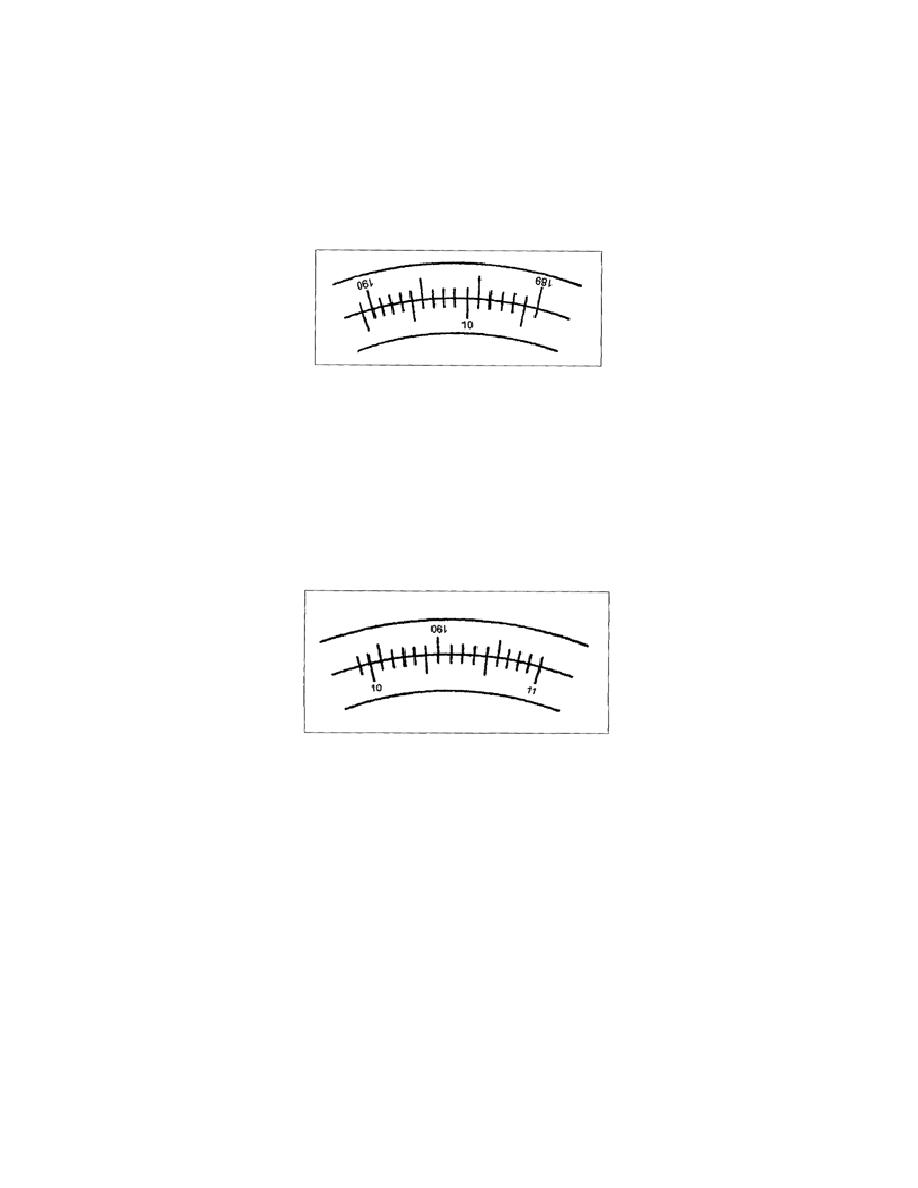
Example 1: When both necessary degree marks show in the circle telescope and the degree mark of the
upper circle is to the right of that of the lower circle, the value is 10 + (6 graduations x 2'), which is
equal to 10 + 12' (Figure 3-9).
Figure 3-9. Determining the Minute Value - Example 1
When the correct or true value for the degrees does not show in the circle telescope, the reading for the
minute value can be made in either of the following two ways.
Example 2: Since 190, from the value showing in the lower circle is to the left in Figure 3-10, the
minute value must be subtracted from the visible degree value to give the true value of the direction.
Therefore, 10 - (9 graduations x 2') is equal to 10 - 18', which is equal to 9 42'.
Figure 3-10. Determining the Minute Value - Example 2
Count to the right the number of divisions from the true degree value on the lower circle (which does not
show) to the value 190, difference on the upper circle. Realizing that from the 9, mark to the 10 mark
on the lower circle there are 15 divisions, count the number of divisions to the right from the 10, mark
on the lower circle to the 189 mark on the upper circle.
9 + (15 graduations + 6 graduations) x 2'
9 + (21 graduations x 2') = 9 + 42'
(4) The previously described methods, using both circles, are slower than methods using the
index mark. However, it is also possible for the index mark to be
3-21
EN0593



 Previous Page
Previous Page
