c. To read the sine or cosine of an angle greater than 45, it is necessary to look at the bottom of
the page reading up instead of down. The column for minutes will be on the right instead of the left. To
find the cosine of 57€ 18', see Figure 4-3. The cosine of 57€ 18' is 0.84151. To find the tangant and
cotangant of an angle, use the same procedure.
d. Often you will be given the sides of a right triangle, and you will want to find the acute
angles of it. Remember that the sine of an angle is equal to the opposite side divided by the hypotenuse.
By making a fraction of the two sides' values, you will get the value of the sine function of the angle.
To find the angle, look up this value in the proper table under the sin column and then read the number
of degrees and minutes in a manner opposite to that used when finding a function for a given angle. For
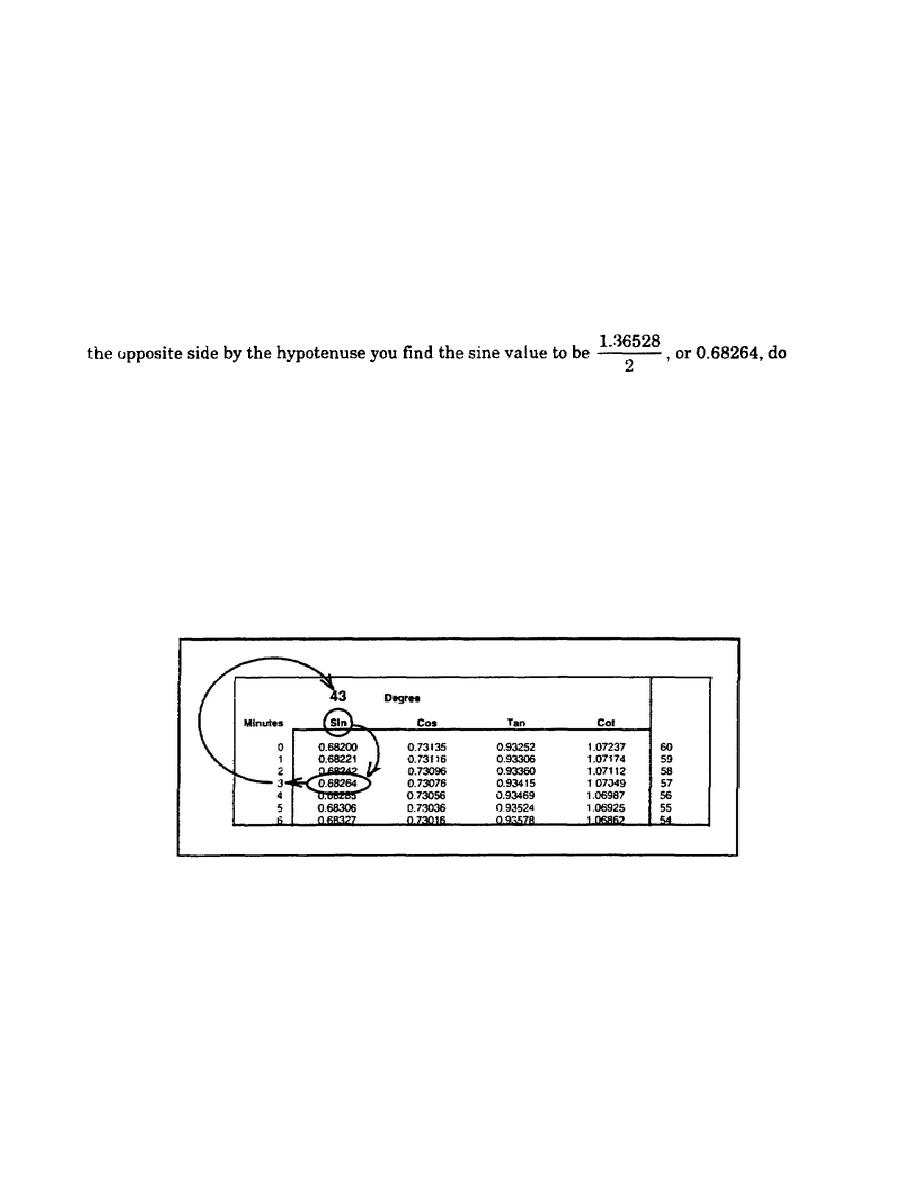
example, if by dividing
the following:
Locate this number under the sin column in Figure 4-4. You find your angle to be 43.
Note that the angle is on the top of the page; therefore, the minute portion of your angle
will be found in the minutes column on the left-hand side of the page. Directly on the
line to the left of 0.68264 in the minutes column, you find 03'. The final answer then
would be 43 03'. This problem would be written in the following manner:
sin A = 0.68264
A = 43 03'
Figure 4-4. Finding the acute angle
e. So far you have learned how to find the functions of angles expressed in degrees and
minutes. However, it is sometimes necessary to find the functions of angles expressed in seconds. This
is done by a process called interpolation. For every change of degrees, minutes, or seconds in an angle,
there is a proportional change in the function of the angle. By the use of this proportion, it is possible to
interpolate for the seconds of an angle.
4-11
EN0591



 Previous Page
Previous Page
