________________________________________________________________Wave Propagation
1-112. Frequency affects both sound and light. A certain range of sound
frequencies produces sensations that you can hear. A slow vibration (low
frequency) in sound gives the sensation of a low note. A more rapid sound
vibration (higher frequency) produces a higher note. Likewise, a certain
range of light frequencies produces sensations that you can see. Violet light is
produced at the high-frequency end of the light spectrum, while red light is
produced at the low-frequency end of the light spectrum. A change in
frequency of sound waves causes an audible sensation--a difference in pitch.
A change in the frequency of a light wave causes a visual sensation--a
difference in color. For a comparison of light waves with sound waves, see
Table 1-2.
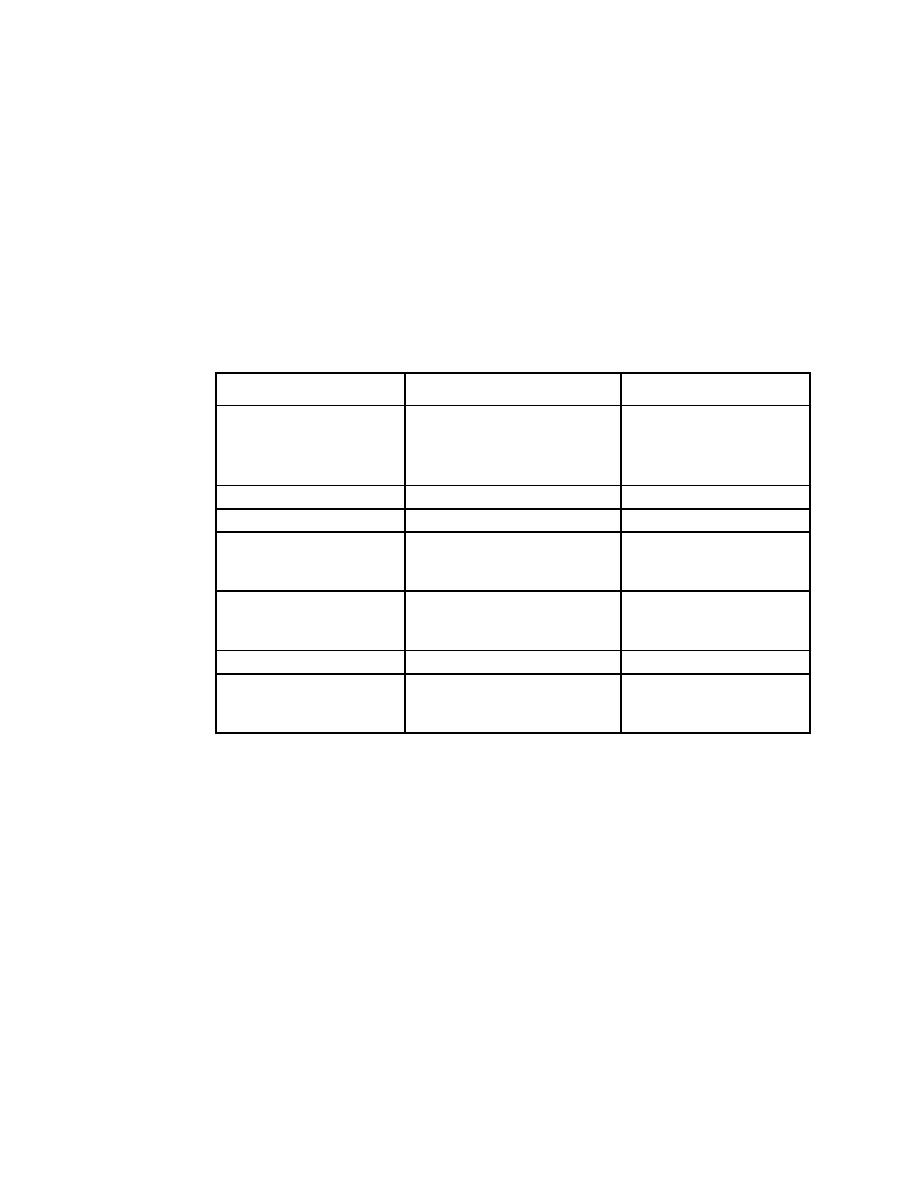
Table 1-2. Comparison of Light Waves and Sound Waves
SOUND WAVES
LIGHT WAVES
Velocity in air
Approximately 1,100 feet per
Approximately 186,000
second.
miles per second
(300,000,000 meters per
second).
Form
A form of wave motion.
A form of wave motion.
Wave composition
Longitudinal.
Transverse.
Transmitting medium
All substances.
Empty space and all
substances except
opaque materials.
Relation of transmitting
The denser the medium, the
The denser the medium,
medium velocity to
greater the speed.
the slower the speed.
velocity
Sensations produced
Hearing.
Seeing.
Variations in
A low frequency causes a low
A low frequency causes
sensations produced
note; a high frequency
red light; a high frequency
causes a high note.
causes violet light.
1-113. Light is one kind of electromagnetic energy. There are many other
types of electromagnetic energy, including heat energy and radio energy. The
only difference between the various types of electromagnetic energy is the
frequency of their waves (rate of vibration). The term spectrum is used to
designate the entire range of electromagnetic waves arranged in order of
their frequencies. The visible spectrum contains only those waves that
stimulate the sense of sight. As a technician, you might be expected to
maintain equipment that uses electromagnetic waves within, above, and
below the visible spectrum.
1-114. There are neither sharp dividing lines nor gaps in the electromagnetic
spectrum. Figure 1-22 illustrates how portions of the electromagnetic spectrum
overlap. Notice that only a small portion of the electromagnetic spectrum
contains visible waves, or light, that can be seen by the human eye.
1-31



 Previous Page
Previous Page
