________________________________________________________________Wave Propagation
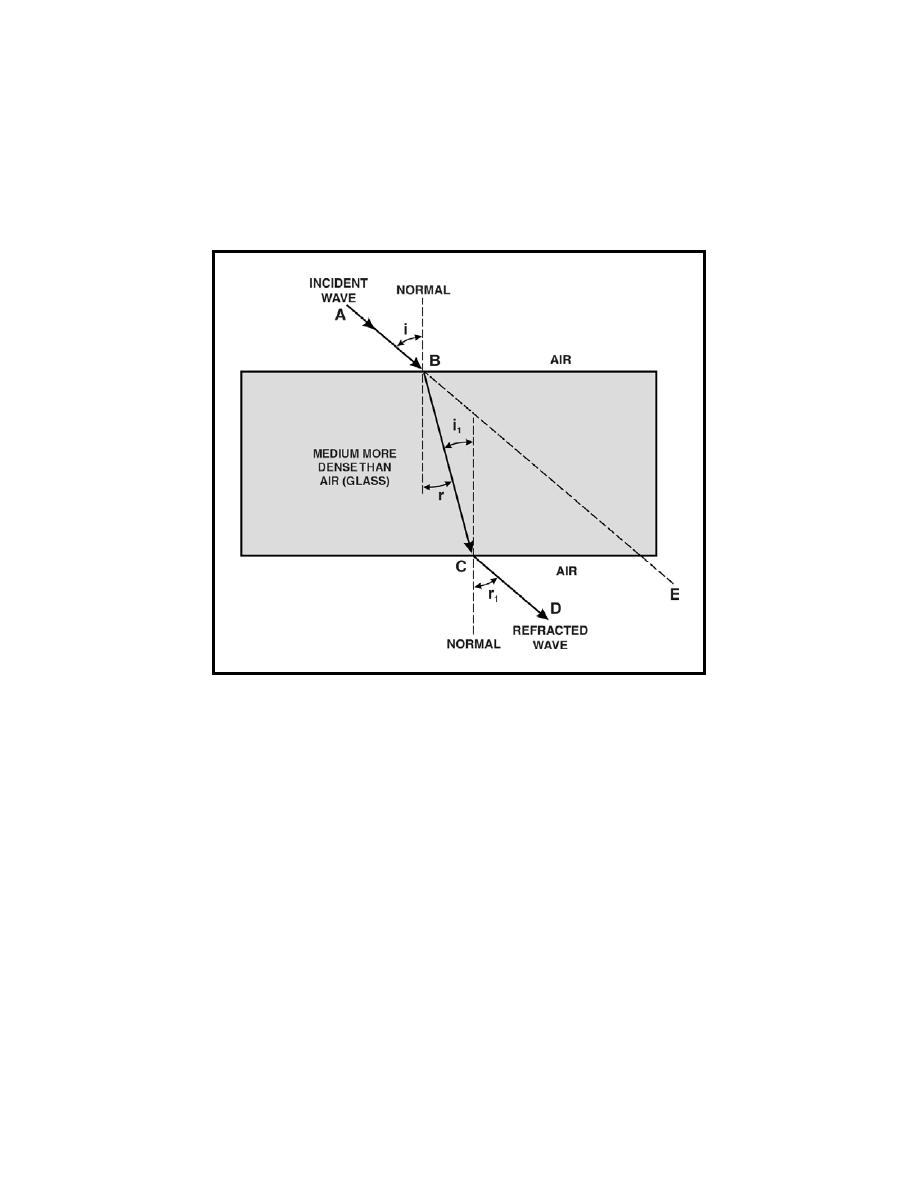
the path from point C to D. As the wave passes through the last boundary, its
velocity increases to the original velocity. As figure 1-10 shows, refracted
waves can bend toward or away from the normal. This bending depends on
the velocity of the wave through each medium. The broken line between
points B and E is the path that the wave would travel if the two mediums (air
and glass) had the same density.
Figure 1-10. Refraction of a Wave
1-41. To summarize what figure 1-10 shows--
If the wave passes from a less dense medium to a denser medium, it
is bent toward the normal, and the angle of refraction (r) is less than
the angle of incidence (i).
If the wave passes from a denser to a less dense medium, it is bent
the angle of incidence (i1).
1-42. You can more easily understand refraction by looking at figure 1-11.
There is a plowed field in the middle of a parade ground. Think of the
incident wave as a company of recruits marching four abreast at an angle
across the parade ground to the plowed field, then crossing the plowed field
and coming out on the other side onto the parade ground again. As the recruits
march diagonally across the parade ground and begin to cross the boundary
onto the plowed field, the front line is slowed down. Because the recruits arrive
at the boundary at different times, they will begin to slow down at different
times (number 1 slows down first and number 4 slows down last in each line).
The net effect is a bending action. When the recruits leave the plowed field and
reenter the parade ground, the reverse action takes place.
1-13



 Previous Page
Previous Page
