________________________________________________________________Wave Propagation
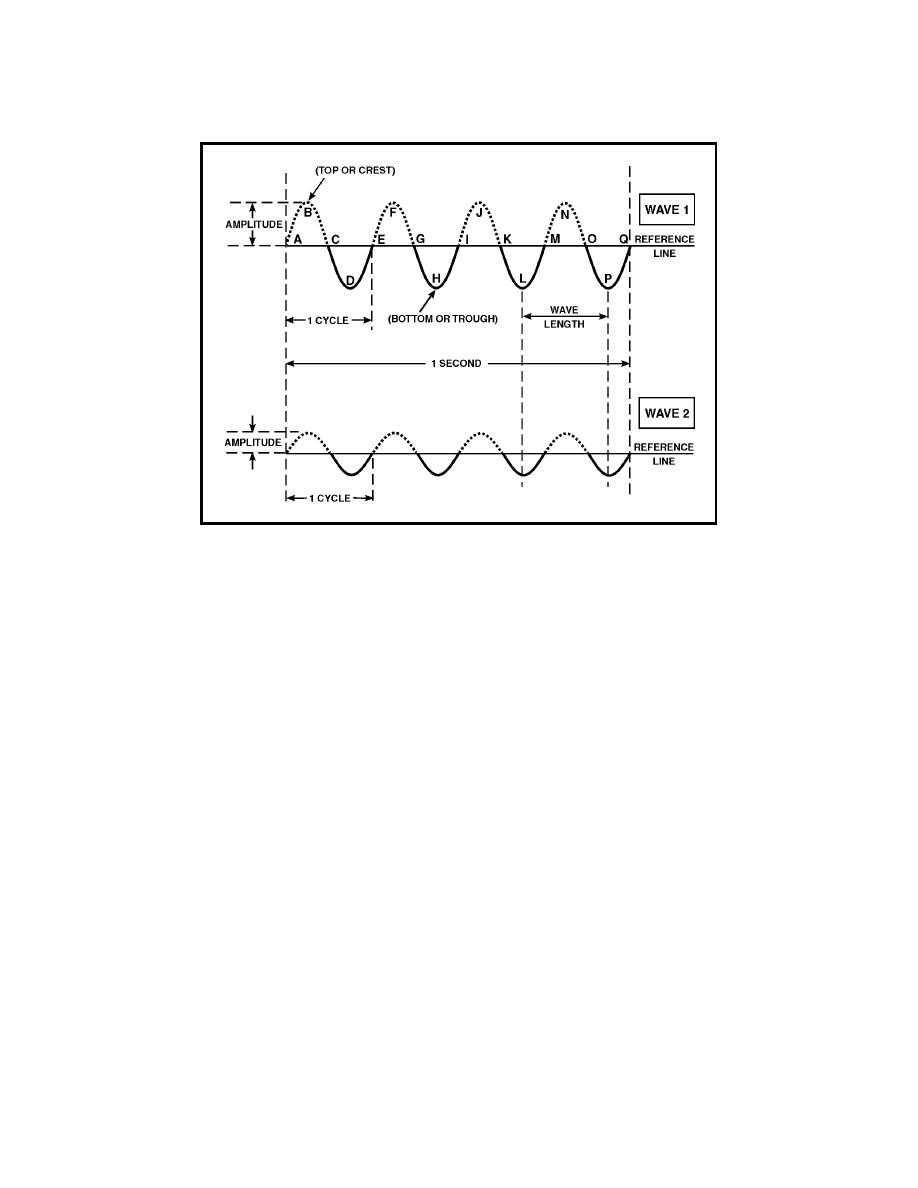
Figure 1-7. Comparison of Waves with Different Amplitudes
Wave Cycles
1-20. Refer to wave 1 in figure 1-7. Notice how similar it is to the sine wave
you have already studied. All transverse waves appear as sine waves when
viewed from the side. In figure 1-7, wave 1 has four complete wave cycles.
Points ABCDE comprise one complete cycle having a maximum value above
and a maximum value below the reference line. The portion above the
reference line (between points A and C) is called a positive alternation and
the portion below the reference line (between points C and E) is known as a
negative alternation. The combination of one complete positive and one
complete negative alternation represents one cycle of the wave. At point E,
the wave begins to repeat itself with a second cycle completed at point I, a
third at point M, and so forth. The peak of the positive alternation (maximum
value above the line) is sometimes referred to as the top or crest, and the
peak of the negative alternation (maximum value below the line) is
sometimes called the bottom or trough, as depicted in the figure. Therefore,
one cycle has one crest and one trough.
Wavelength
1-21. A wavelength is the distance in space occupied by one cycle of a radio
wave at any given instant. If the wave could be frozen in place and measured,
the wavelength would be the distance from the leading edge of one cycle to
the corresponding point on the next cycle. Wavelengths vary from a few
hundredths of an inch at extremely high frequencies to many miles at
extremely low frequencies; however, common practice is to express
wavelengths in meters. In figure 1-7 (wave 1), the distance between A and E,
or B and F, etc., is one wavelength. The Greek letter lambda (λ) is used to
signify wavelength. Why lambda and not "l" or "L"? This is because "L" is
1-7



 Previous Page
Previous Page
