Figure 4-15. Angles between 270 and 360
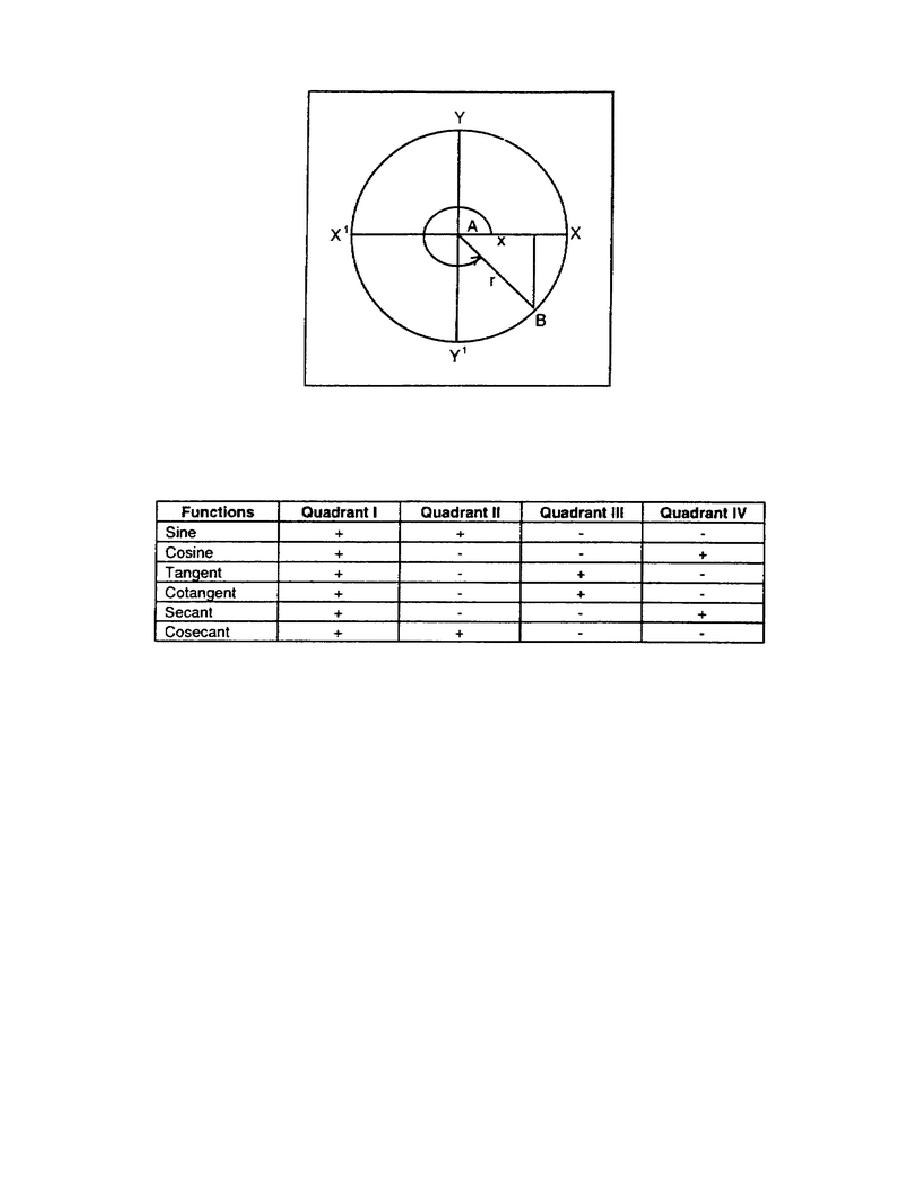
j. Table 4-2 shows the relationship of the sign, the function, and the quadrant of an angle.
Table 4-2. Relationship of the sign, the function, and the quadrant
4-7. The Unit Circle. If a circle has a radius of unity, then the numerical values of the functions for a
given angle are represented by the lengths of the lines. This is illustrated for a second-quadrant angle in
Figure 4-16.
4-8. Oblique Triangles. Many incidences arise in your daily work that deal with the solution of
oblique triangles. To solve these triangles, the fundamental principles of the functions of angles greater
than 90€ must be understood. The functions of angles greater than 90€ can be expressed as the functions
of acute angles. These acute angles are found by subtracting the given angle from-
180 for quadrant II.
270€ for quadrant III.
360€ for quadrant IV.
EN0591
4-22


 Previous Page
Previous Page
