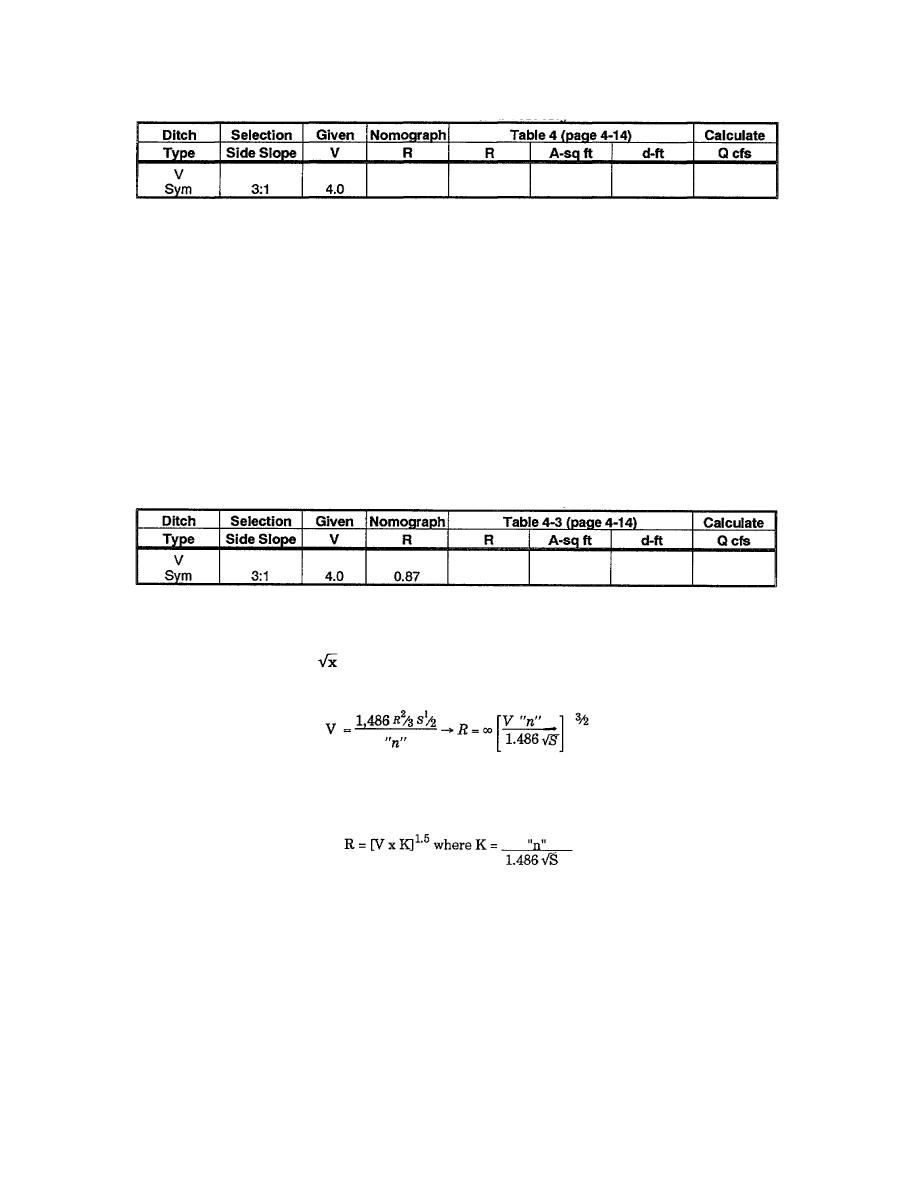
Table 4-5. First trial velocity
Using the nomograph in figure 4-5, we must first locate a turning point on the turning line. This line is the center
line on the nomograph. The turning point is found by locating the slope(s) in ft/ft in the column at the far left of
the chart and the roughness coefficient ("n") on the far right column and connecting them with a straight line.
Where the line crosses the turning line is the turning point. This turning point will remain the same as long as S
and "n" do not change.
NOTE: Another method using the Manning Equation with a calculator is shown below.
The hydraulic radius is found by connecting the velocity in the second column from the right, and the turning
point by a straight line through to the R scale and reading the hydraulic radius (R) off the second column from the
left. This gives the required R for any given V in Manning's Equation. In this example, R equals 0.87 which
shows the calculator method for solving the radius.
Table 4-6. Calculated radius
Determining the Hydraulic Radius Using Manning's Equation
and yx, you can determine R more quickly and accurately than with the
If your calculator has the function
nomograph provided in the workbook Transposing Manning's Equation,
Since n and S are constant for various trial iterations, you need only enter different values for V to arrive at an
acceptable value for R. Therefore, if S and n are constant, the above equation for R becomes:
To calculate R, use the above equation for numerous iterations until you have "bracketed" flowrate Q within
acceptable limits. Below are keystrokes which will work on most calculators.
EN5465
4-16



 Previous Page
Previous Page
