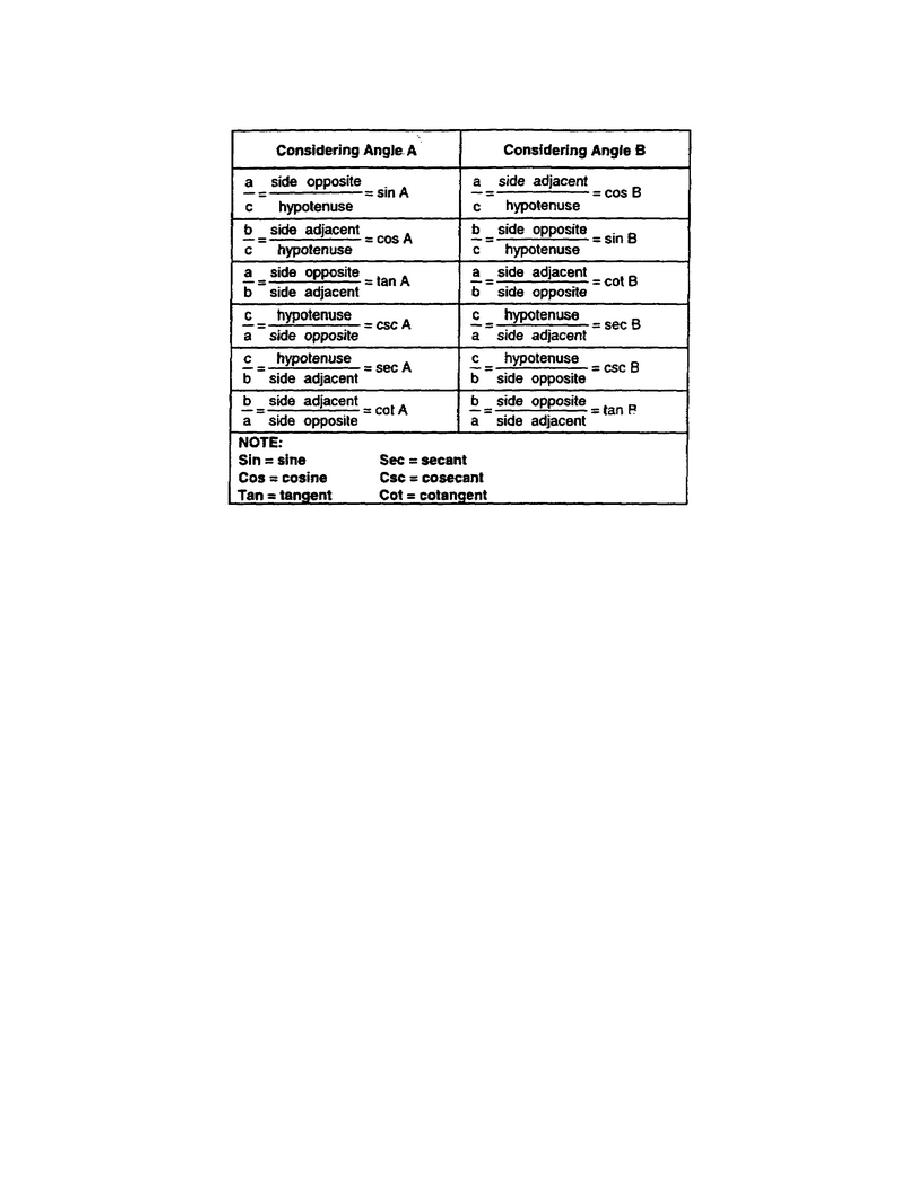
Table 4-1. Special names for ratios
4-5. Functions of Trigonometry. If A is any given angle, a set of values can be determined for the six
ratios. Because they will vary with the changes in A, the sine A, cosine A, tangent A, cotangent A,
secant A, and cosecant A are functions of A and are specifically referred to as trigonometric functions.
See Appendix C for the Natural Trigonometric-Functions Tables.
a. In general, the decimal form of a function is an endless decimal. By the use of advanced
mathematics, an angle's function can be computed to as many decimal places as desired. In any table of
function values, the error in any entry is at most one-half of a unit in the last place. A natural
trigonometric-functions table may show 4 to 10 place values and is easy to use. Because of the
complementary relationship of the acute angles in a right triangle, that is, sine A = cosine (90-A) and so
forth, each entry in a natural trigonometric-functions table serves a dual purpose and, consequently, the
table is only one-half as large as it otherwise would be.
b. Figure 4-3, page 4-10, is an example of a natural trigonometric-functions table. From this
table, find the sine 32 20' using the procedures below:
Locate the page with 32 at the top.
Find the sin and cos columns under 32.
Locate the word minutes at the left of the page. Going down this column, go to 20'.
Go right across this line to the sin column. There you will find 0.53484, which is the sine
of 32 20'.
4-9
EN0591




 Previous Page
Previous Page
