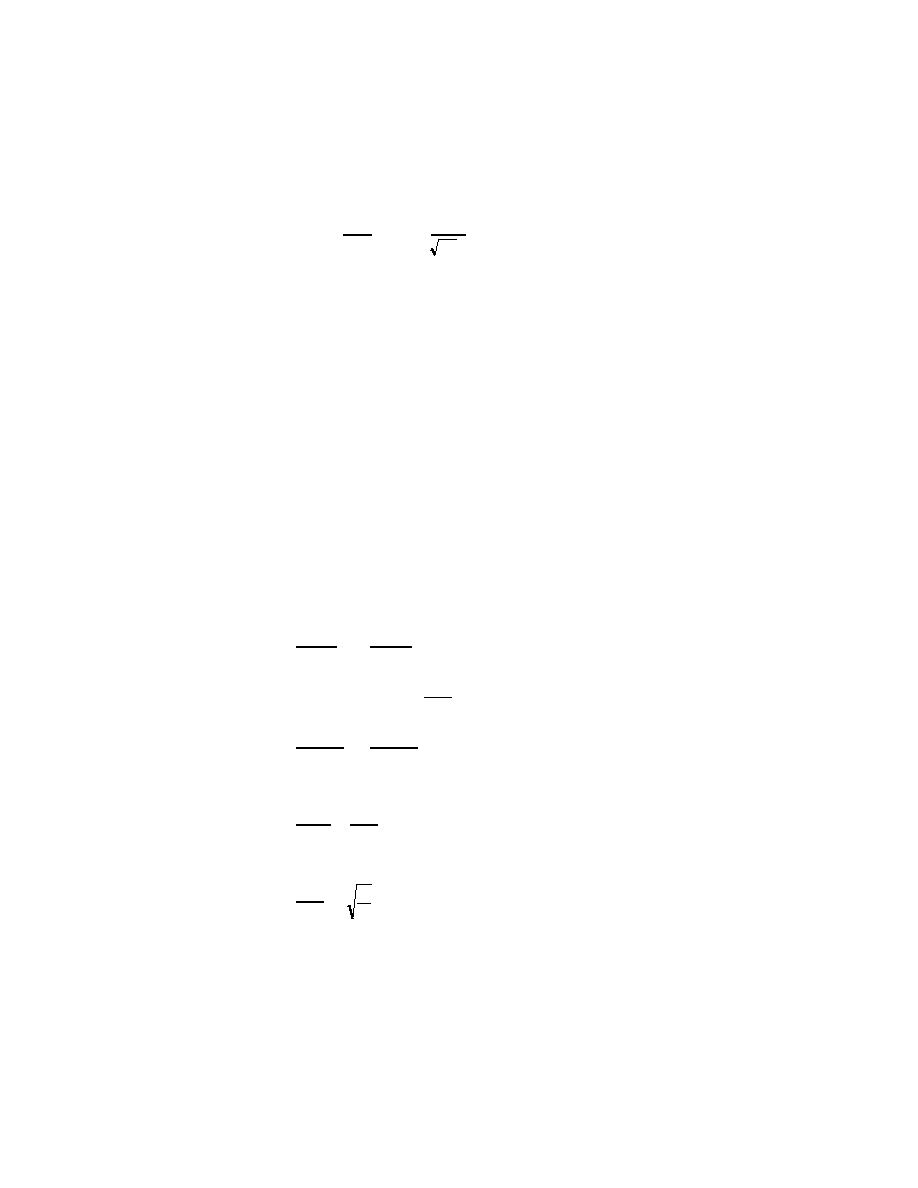
TC 9-64 _________________________________________________________________________
3-84. This final equation is used for finding the time required for a voltage
change to travel a unit length, because L and C are given in terms of unit
length. The velocity of the waves may be found by the following equation,
where D is the physical length of a unit:
D
D
v=
Or v =
T
LC
3-85. This is the rate at which the wave travels over a unit length. The units
of L and C are henrys and farads, respectively. T is in seconds per unit length
and V is in unit lengths per second.
3-86. As previously discussed, an infinite transmission line exhibits a definite
input impedance. This impedance is the characteristic impedance and is
independent of line length. The exact value of this impedance is the ratio of
the input voltage to the input current. If the line is infinite or is terminated
in a resistance equal to the characteristic impedance, voltage and current
waves traveling the line are in phase. Recall the following equations:
ET = LI
IT = CE
To determine the characteristic impedance or voltage-to-current ratio, use the
following procedure:
Divide the equations:
ET = LI and IT = CE
ET
LI
=
IT
CE
E
Multiply the result by
I
E2T
LIE
=
I2T
CEI
Simplify:
E2
L
=
I2
C
Take the square root:
E
L
=
= Z0 (characteristic impedance)
C
I
3-87. A problem using this equation illustrates how to determine the
characteristics of a transmission line.
3-26




 Previous Page
Previous Page
