_____________________________________________________________________ Special Amplifiers
So point A is at virtual ground in this circuit also. To check the results, compute the
voltage at V2 as follows:
V2 = (voltage at point A) - ER2
V2 = (0 V) - ( +10 V)
V2 = -10 V
You can compute the values for view (C) and prove that point A in that circuit is also at
virtual ground.
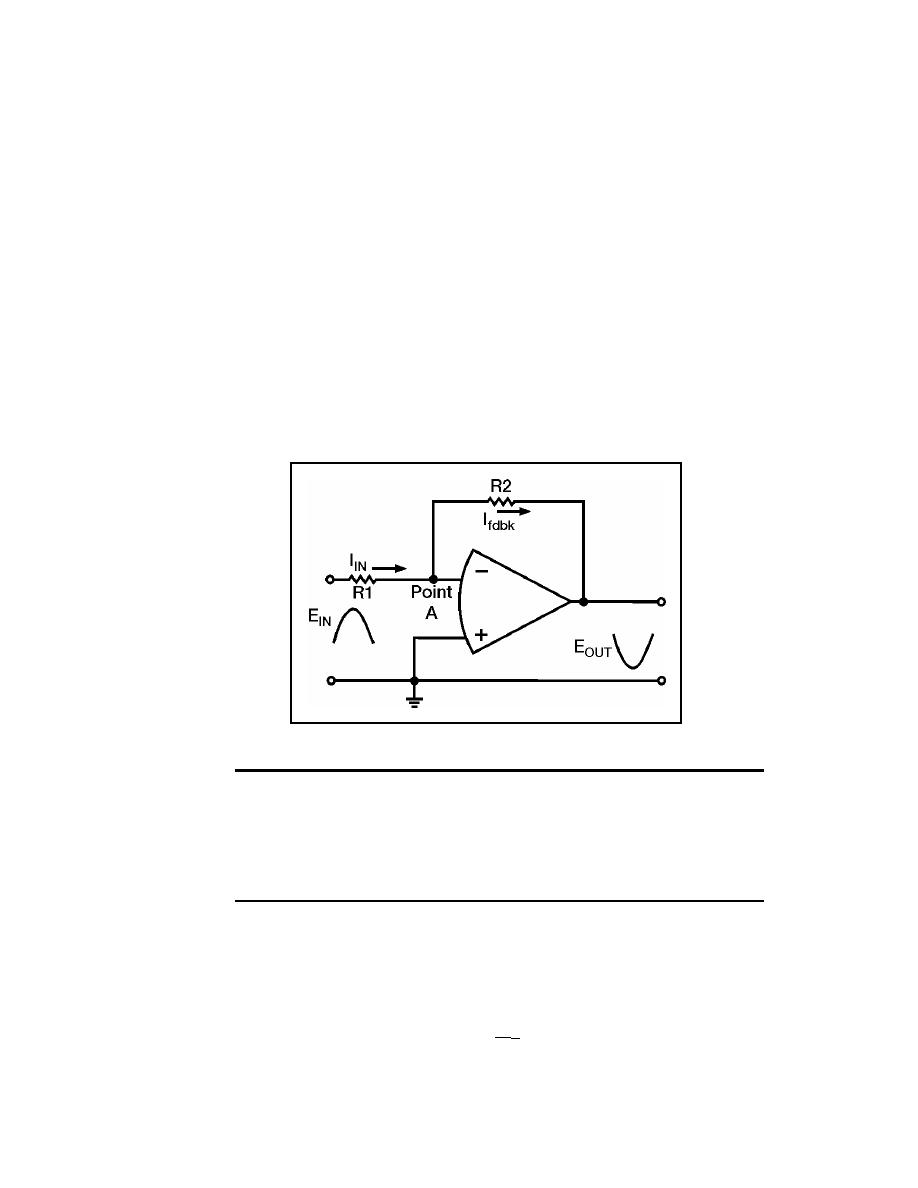
7-63. The whole point is that the inverting input to the operational amplifier shown in
Figure 7-12 (for all practical purposes) is at virtual ground since it is at 0 volts. Since the
inverting input is at 0 volts, there will be no current (for all practical purposes) flowing into
the operational amplifier from the connection point of R1 and R2.
7-64. Given these conditions, the characteristics of this circuit are determined almost
entirely by the values of R1 and R2. Figure 7-14 should help show how the values of R1
and R2 determine the circuit characteristics.
Figure 7-14. Current Flow in the Operational Circuit
NOTE: It should be stressed at this point that for purpose of explanation, the
operational amplifier is a theoretically perfect amplifier. In actual practice we
are dealing with less than perfect. In the practical operational amplifier there
will be a slight input current with a resultant power loss. This small signal can
be measured at the theoretical point of virtual ground. This does not indicate
faulty operation.
7-65. As shown in Figure 7-14, the input signal causes current to flow through R1. Only
the positive half cycle of the input signal is shown and will be discussed. Since the voltage
at the inverting input of the operational amplifier is at 0 volts, the input current (IIN) is
computed by using the following formula:
IIN = EIN
R1
23 June 2005
TC 9-62
7-19




 Previous Page
Previous Page
